- 現在位置
- トップ > 教育 > 小学校、中学校、高等学校 > 教科書 > 教科書の改善・充実に関する研究報告書について > 教科書の改善・充実に関する研究報告書(算数)-平成18、19年度文部科学省委嘱事業「教科書の改善・充実に関する研究事業」- > 第1章 6.「数量関係」領域における教科書記述の研究
第1章 6.「数量関係」領域における教科書記述の研究
「数量関係」領域における教科書記述の研究として実施した、ワーキンググループの報告内容は以下の通りである。
1.総論
(1)数量関係の分量比較
平成10年告示の学習指導要領で数量関係は、小学校第3学年から第6学年にかけて位置づけられている。
教科書分析をする際に、質的な側面と量的な側面の2つの方法が考えられる。以下では、数量関係領域が充実していたと思われる昭和40年代、50年代と現在の教科書について量的な比較をしてみたい。
取り上げる教科書は、A社のみである。これは、それぞれの時代の他の教科書が手に入らなかったことによる。
昭和43年告示の学習指導要領に基づく教科書として、昭和45年検定の算数教科書、52年告示の同書に基づく教科書として、昭和54年検定の同教科書、平成10年告示の同書に基づく教科書として、平成16年検定の同教科書を比較する。それぞれの総頁数と数量関係領域のページ数は以下の通りである。
図表1-26 教科書の頁数の比較
| 昭和45年検定教科書 | 昭和54年検定教科書 | 平成16年検定教科書 | |
|---|---|---|---|
| 小3~小6の算数教科書の総頁数 | 1,040 | 804 | 762 |
| 小3~小6の数量関係の総頁数 | 214 | 140 | 84 |
- 教科書の総頁数は小3上~小6下の8冊の頁数の和。数量関係の総頁数は、単元のみである。教科書の終わりや単元と単元の間にある練習問題等は含めてない。
昭和54年検定教科書と平成16年検定教科書の総頁数は、ほとんど同じと見てよい。これは、昭和45年と54年の教科書がA5版であるのに対して、平成16年の教科書がB5版であるからである。しかしながら、昭和45年検定教科書と比較した場合、昭和54年ならびに平成16年検定教科書は総頁数が約2割減となっていることがわかる。
一方、数量関係の頁数は、大幅に減少していることがわかる。これは、平成16年検定教科書では、数量関係の内容が大幅に少なくなったことが主な原因であろう。例えば、昭和45年検定教科書と昭和54年検定教科書で扱っていた、文字と式、反比例、変わり方を表す式やグラフ、場合の数やちらばり具合等の資料の調べ方が平成16年検定教科書では、なくなったことによる。
平成10年告示の学習指導要領解説算数編によれば、数量関係領域のねらいは、「『A数と計算』、『B量と測定』、『C図形』の各領域の内容を理解したり、活用したりする際に用いられる数学的な考え方や方法を身に付けることである」という。数量関係領域の特に統計関係内容が削除されている現在の教科書は、活用を重視する今日的課題からしても、算数数学教育がねらう数学的見方・考え方の育成の観点からも問題であることがわかる。
(2)数量関係の内容の検討
数量関係のワーキンググループでは、数量関係領域を中心として第4学年から第6学年にかけて指導すべき見方・考え方でありながら児童に身についていないものとして、比例の見方があると考えるに至った。
用語「比例」ならびにその定義は6学年で指導される。一方で比例の見方は、算数学習の様々な場面に存在する。しかしながらそれらが暗黙のうちに用いられることもあって、なかなか顕在化しない。顕在化させないまま学習が進むためその見方が身につかず、結果的に活用できるようになっていない。以下では、数量関係以外の領域でその背景にある比例の見方について考えてみたい。
まずは数と計算領域で考えてみる。
乗法・除法の意味指導では、用いられる場面の前提としてあるのは比例関係である。整数の乗法・除法の意味場面から比例の見方を顕在化させ、段階的に指導していくべきと考える。以下の問題場面は、3学年の整数![]() 整数の立式場面である。
整数の立式場面である。
1メートルのねだんが312円のリボンを、3メートル買いました。
代金はいくらですか。
(A社3下)
この問題では、312![]() 3と立式して問題を解決するはずである。乗法を用いることの根拠は、3メートル買ったときのどの1メートルもその値段が312円であることを前提としている。日常生活ではまとめて購入すると1メートルあたりの値段は安くなることが多い。しかし算数では、長さが長くなっても同じ単価であることを前提に考える。言い換えれば、1メートルあたりの値段と長さが比例関係にあることを前提に乗法を用いるのである。もしもこの前提が(暗黙ではあっても)認められなければ、312
3と立式して問題を解決するはずである。乗法を用いることの根拠は、3メートル買ったときのどの1メートルもその値段が312円であることを前提としている。日常生活ではまとめて購入すると1メートルあたりの値段は安くなることが多い。しかし算数では、長さが長くなっても同じ単価であることを前提に考える。言い換えれば、1メートルあたりの値段と長さが比例関係にあることを前提に乗法を用いるのである。もしもこの前提が(暗黙ではあっても)認められなければ、312![]() 3と立式して代金を求めることはしないだろう。
3と立式して代金を求めることはしないだろう。
これは、第5学年の整数![]() 整数の立式場面でも同じである。
整数の立式場面でも同じである。
式をかいて答えを求めましょう。
(ア) 4メートルが30グラムのはり金1メートルの重さ
(B社5上)
この問題を30![]() 4と立式して解決する前提には、長さがn倍になれば重さもn倍になるという前提がある。この前提のもと、30グラムの重さの4等分が1メートルの重さであると考えたり、1メートルの重さを
4と立式して解決する前提には、長さがn倍になれば重さもn倍になるという前提がある。この前提のもと、30グラムの重さの4等分が1メートルの重さであると考えたり、1メートルの重さを![]() 円として4メートルの代金は1メートルの4倍と考え、
円として4メートルの代金は1メートルの4倍と考え、![]()
![]() 4
4![]() 30として
30として![]()
![]() 30
30![]() 4として求めているはずである。ここでも、長さと重さが比例関係にあることを前提に除法を用いているのであって、この前提を(暗黙ではあっても)認めないかぎり30
4として求めているはずである。ここでも、長さと重さが比例関係にあることを前提に除法を用いているのであって、この前提を(暗黙ではあっても)認めないかぎり30![]() 4と立式することはないだろう。
4と立式することはないだろう。
次に、量と測定領域で考えてみたい。
5学年で学習する平行四辺形の面積公式は以下のようである。
平行四辺形の面積![]() 底辺の長さ
底辺の長さ![]() 高さ
高さ
平行四辺形の面積公式が上のような言葉の式としてまとめられたということは、平行四辺形の面積は底辺が一定のとき高さに比例し、高さが一定のとき底辺の長さに比例していることを表しているはずである。一部の教科書は、表にまとめて規則性を確認しているが、式のよみとして、あるいは言葉の式が表す意味としてぜひとも指導したい内容である。
このことは、6学年で学習する立方体や直方体の体積公式でも同じである。
直方体の体積![]() 縦
縦![]() 横
横![]() 高さ
高さ
このように公式としてまとめられるということは、直方体の体積が縦![]() 横できまる底面積(実際は底体積)が一定のとき高さに比例し、高さが一定のときは縦
横できまる底面積(実際は底体積)が一定のとき高さに比例し、高さが一定のときは縦![]() 横できまる底面積(同)に比例することを表しているのである。
横できまる底面積(同)に比例することを表しているのである。
これは、円周率を導いた次の言葉の式においても同じである。
円周の長さ![]() 直径
直径![]() 円周率
円周率
実際の指導では、筒状の形の周の長さを測り、これらを表にまとめ規則性を見つける活動を行う。完成した表の縦の対応の規則を考えると、円周の長さ![]() 直径が一定の値となることに気づく。これが円周率の意味である。数学的に円周率は比例定数であり、円周の長さが直径に比例していることを表している。
直径が一定の値となることに気づく。これが円周率の意味である。数学的に円周率は比例定数であり、円周の長さが直径に比例していることを表している。
このように数量関係以外でも比例の見方・考え方は様々な場面で出てきており、これらの見方・考え方を育てる紙面構成が必要であると考える。逆に言えば、紙面構成で見せていかない限り、比例の見方・考え方を育てる意識が教員自身に根付かないのではないかと考える。
本ワーキンググループは、数量関係領域を検討することが目的である。そこで、以下では、数量関係の領域について4、5、6の各学年で比例の見方を強調した紙面構成を提案することを意図して、現在の教科書の現状と改善案について分析してみたい。
2.第4学年 「変わり方調べ」「変わり方」「ともなって変わる量」
(1)教科書記述の分析
 「変わり方調べ」の扱われ方
「変わり方調べ」の扱われ方
4年の数量関係の単元において「どのような関係が取り上げられているのか」、「「対応」と「変化」がどのように取り上げられているのか」、「変化の様子を表す折れ線グラフがどのように取り上げられているのか」について分析を行った。
[A社]
![]() 時刻あてゲーム(2つの時計盤の時刻の関係)
時刻あてゲーム(2つの時計盤の時刻の関係)
ここでは和が一定の関係を取り上げている。この関係はy![]()
![]() x
x![]() 13と見ることができる。また、この関係を言葉の式、
13と見ることができる。また、この関係を言葉の式、![]() と
と![]() を使った式に表している。
を使った式に表している。

![]() 正三角形の個数とまわりの長さ
正三角形の個数とまわりの長さ
ここでは差が一定の関係を取り上げている。この関係は一次関数y![]() x
x![]() 2と見ることができる。また、この関係を
2と見ることができる。また、この関係を![]() と
と![]() を使った式に表している。
を使った式に表している。

![]() 正方形を階段にならべたときの、だんの数とまわりの長さ
正方形を階段にならべたときの、だんの数とまわりの長さ
ここでは比例関係(y![]() 4x)を取り上げている。
4x)を取り上げている。
![]()
![]() たての長さが3センチメートルの長方形の、横の長さと面積
たての長さが3センチメートルの長方形の、横の長さと面積
ここでは比例関係(y![]() 3x)を取り上げている。また、この関係を
3x)を取り上げている。また、この関係を![]() と
と![]() を使った式に表している。
を使った式に表している。

[B社]
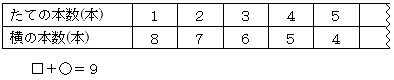
![]() 18本のひごでつくった長方形の、たての本数と横の本数
18本のひごでつくった長方形の、たての本数と横の本数
ここでは和が一定の関係を取り上げている。この関係はy![]()
![]() x
x![]() 9と見ることができる。また、この関係を
9と見ることができる。また、この関係を![]() と
と![]() を使った式に表している。
を使った式に表している。
![]() 正方形を階段にならべたときの、だんの数とまわりの長さ
正方形を階段にならべたときの、だんの数とまわりの長さ
ここでは比例関係(y![]() 4x)を取り上げている。また、この関係を
4x)を取り上げている。また、この関係を![]() と
と![]() を使った式に表している。
を使った式に表している。

![]() 水そうに水を入れていったときの水のかさと全体の重さ
水そうに水を入れていったときの水のかさと全体の重さ
ここでは差が一定の関係を取り上げている。この関係は一次関数y![]() x
x![]() 0.5と見ることができる。また、この関係をグラフにかくことを取り扱っている。(式は取り扱っていない。つまり式とグラフの対応はない。)
0.5と見ることができる。また、この関係をグラフにかくことを取り扱っている。(式は取り扱っていない。つまり式とグラフの対応はない。)

[C社]
![]() 正三角形の数とストローの数
正三角形の数とストローの数
ここでは一次関数y![]() 2x
2x![]() 1が取り上げられている。2つの量の対応より2本ずつ増えるという変化が強調されている。
1が取り上げられている。2つの量の対応より2本ずつ増えるという変化が強調されている。
![]()
![]() 正方形の数とストローの数
正方形の数とストローの数
ここでは一次関数y![]() 3x
3x![]() 1が取り上げられている。2つの量の対応より3本ずつ増えるという変化が強調されている。
1が取り上げられている。2つの量の対応より3本ずつ増えるという変化が強調されている。
![]()
![]() 階だんの数と下からの高さ
階だんの数と下からの高さ
ここでは比例関係(y![]() 15x)を取り上げている。また、この関係を
15x)を取り上げている。また、この関係を![]() を使った式に表している。
を使った式に表している。
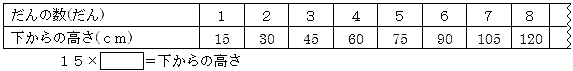
![]() 水を入れた時間とたまった水の量
水を入れた時間とたまった水の量
ここでは比例関係(y![]() 1.5x)を取り上げている。時間は2分毎で、0分の場合を表記している。また、この関係をグラフにかくことを取り扱っている。(式は取り扱っていない。つまり式とグラフの対応はない。)
1.5x)を取り上げている。時間は2分毎で、0分の場合を表記している。また、この関係をグラフにかくことを取り扱っている。(式は取り扱っていない。つまり式とグラフの対応はない。)
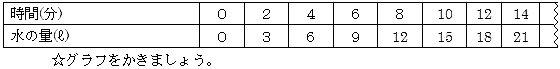
![]() 水を入れた時間とたまった水の量
水を入れた時間とたまった水の量
ここでは比例関係(y![]() 0.75x)を取り上げている。原点を含めてグラフをかき、
0.75x)を取り上げている。原点を含めてグラフをかき、![]() の問題のグラフとの比較を取り扱っている。時間は4分毎で、0分の場合を表記している。(式は取り扱っていない。)
の問題のグラフとの比較を取り扱っている。時間は4分毎で、0分の場合を表記している。(式は取り扱っていない。)

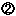 考察
考察
各社とも工夫された素材を取り入れている。特にあつ紙、ひご、ストローなどを用い、具体的な算数的活動を可能にしている素材は4年生の児童にとってわかりやすい。今後も工夫を期待する。
各社とも比例する素材だけでなく、他のきまりをもつ素材を取り入れ、対応や変化を捉えさせようとしている。それは良いことではあるが、B社の![]() 、C社の
、C社の![]() 、
、![]() は初めて変わり方を学習する児童にとってやや難解かと思われる。4年ではシンプルな事例で対応と変化を捉えさせたい。
は初めて変わり方を学習する児童にとってやや難解かと思われる。4年ではシンプルな事例で対応と変化を捉えさせたい。
表の扱いに各社とも工夫が見られる。表に完成させる前に、時計盤と時刻の対応を見せる(A社)、組をまずかく(B社)、カードを並べる(C社)というように、独自の工夫が見られる。表の導入にあたっては、このような方法を大いに取り扱うべきである。
グラフの取り扱いには差が見られる。B社、C社は変わり方の単元内でグラフを取り扱っているが、A社は同一単元に取り扱っていない。同一単元で、変化の様子を表すものとしてグラフを取り扱っておきたい。B社のような一次関数はやや難解である。B社の![]() はグラフをかくにあたり原点の扱いを避けたものと思われる。
はグラフをかくにあたり原点の扱いを避けたものと思われる。
式の扱いにも差が見られる。これは指導要領の解釈の違いが現れたものと思われ、新指導要領のもとでは各社とも式表示が強化されてくるものと思われる。きまりを式に表し、活用していくことは大切にしたい。
 提言
提言
比例をふくめ、他の変化の事例を取り上げながら学習する現在の方法を踏襲したいが、同時に難解な事例をさけるようにもしたいと考える。取り扱う範囲は、比例関係と和一定等が望ましいと考える。対応、変化ともに捉えやすく、式に表現しやすいからである。
比例の見方の強化につなげるには、表から対応と変化を捉えさせることが大切である。つまり「たてに見てどんな対応のきまりがあるのか」と「横に見てどんな変化のきまりがあるのか」が見つけられるようにしておきたいと考える。
例えば次のような事例を考えてみる。
![]()
対応とは表の上下の関係である。この上下の対応を基に表が出来上がっているわけで、大切な関係である。変化とは横の見方で、この場合「だんの数が1増えれば、回りの長さは4増える」ことが分かる。この両方の見方を大切にすることが、比例を捉えるために必要である。なお、関係を捉える時には「倍関係」に目が向くようにしておきたい。この例の場合「だんの数が2倍になればまわりの長さも2倍になること」を捉えさせておくことが大切であると考える。この部分を教科書において強化されることを望みたい。
また、グラフ(折れ線グラフ)の活用を図りたい。変化の様子を表すものとして折れ線グラフを用い、点をつないでかくこと、グラフが直線になることを捉えさせておきたい。また、グラフから簡単な数値を読み取る程度の扱いは行いたい。
例えば水槽に水を入れたときの水の量と深さを調べてみるとする。
![]()
このときの折れ線グラフは、各点を結んだものとなるが、それが直線であることを捉えられるようにする。なお、式を示し、式とグラフの関係を取り扱うことはないようにする。図表1-27のように、グラフを取り扱うことが、比例の見方の強化になると考えている。
図表1-27 グラフの例
3.第5学年-割合の導入
比例の見方を顕在化し系統的に指導する場面として第5学年では、割合の導入場面に注目したい。
(1)教科書記述の分析
 「割合」の導入場面での扱われ方
「割合」の導入場面での扱われ方
教科書では、A社がバスケット4チームの勝率の比較、B社が体験学習の定員に対する希望者の比較、C社が1人のバスケットのシュートの成功率の比較から導入している。具体的な場面は以下の通りである。
〔A社〕
| チーム | 試合数 | 勝った数 | 星取り表(○…勝ち ●…負け) |
|---|---|---|---|
| 赤 | 12回 | 6回 | |
| 黄 | 15回 | 6回 | |
| 青 | 10回 | 7回 | |
| 緑 | 15回 | 9回 |
主発問:上の表の4つのチームの中で、どのチームがよく勝っているといえるでしょうか。
〔B社〕
| 教室 | 定員 | 希望者 |
|---|---|---|
| ソーセージづくり | 20人 | 40人 |
| パンづくり | 25人 | 45人 |
| ちちしぼり | 15人 | 21人 |
| バターづくり | 15人 | 12人 |
主発問:定員と比べて希望者の多いのはどの教室かな。
〔C社〕
○は入った。
×は入らなかった。
| 2月10日 | |
|---|---|
| 2月13日 | |
| 2月15日 |
主発問:何日が、いちばん成績がよかったといえるでしょうか。
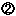 考察
考察
割合とは、比例を前提とした比べ方の1つである。具体的には、もとにする量がそろっていないとき、それに対する比べる量の比率(商)で比較するアイデアである。教科書3社の導入場面で、もとにする量が揃っていない場合にどのように比べてよいのかを問題としているのはそのためである。この際に注意しなければいけないことは、もとにする量と比べる量が比例関係にあることを仮定して推論していることである。
A社の導入場面で言えば、それぞれのチームの試合数に対する勝利の割合が一定、つまりは比例することを仮定するからこそ、それぞれのチームの試合数に対する勝利する割合で比較できるのである。これはB社もC社の場面も同様である。
日常生活では、もとにする量がそろっていないときでも差で比較する場合はある。プロ野球のシーズン記録でいうならば、打率は割合で比較するが、打点やホームラン数は差(絶対量)で比較する。日常の事象を数理的に解決することを教えたい算数科の目標からすれば、差で比較する場合と割合で比較する場合の両方を考え、目的に応じて比べ方を選択していることに触れたい。そうすることによって、割合が比例を前提としていることを顕在化させたいと考える。前述した三社の教科書においてもこのことは十分に考慮されて構成されていると考えるが、差で比較した場合と倍で比較した場合の視点の違いがわかりづらいのではないかと考える。
(2)提言
本稿では、割合で比較するとは、2つの数量関係をそれぞれ一方の数量をもとにして相対的大きさで表す比べ方であり、もとにする量がそろっていなくても比較できるようにした点で数量の処理の仕方として上手い方法であることをさらに強調したいと考える。
比例の見方を顕在化させる場面としては、意図的に仮定して比較する場合よりも素材に内在する場合の方が児童になじみがあると考え、以下では、ゴムの伸びを比較した展開を考えてみたい。
◎どちらの色のゴムの方がよく伸びるゴムといえますか。
| もとの長さ | 伸ばした全体の長さ | |
|---|---|---|
| 青いゴム | 20センチメートル | 50センチメートル |
| 白いゴム | 30センチメートル | 72センチメートル |
ゴムの伸びは、差で比較する方法と倍で比較する方法の2つの方法が考えられる。
差で比較するとは、「伸びた」長さを比較する方法であり、倍で比較するとは、「伸び方」を比較する方法である。これらの比較の際には、それぞれの比べ方を特徴づけるような図表示と関連づけて指導する展開としたい。以下は差で比較する場合である。
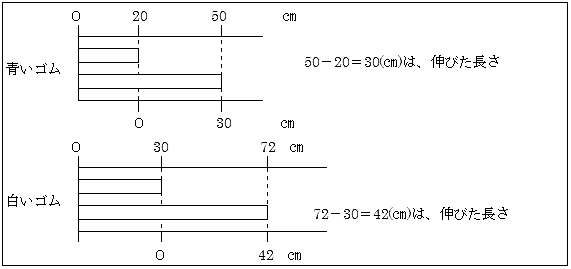
差と対立する方法として倍で比較するがすぐに出てくるとは限らない。そこで強調したいのは、もとの長さをそろえるというアイデアである。これは差的にも倍的にも見ることができるが、倍的に見る考えの10センチメートルあたりの伸びで比較する場合で考えてみたい。
もとにする量をそろえるには、公倍数の考えを用いてそれぞれのもとの長さを60センチメートルにそろえる考え方もあるが、ここでは、それぞれのもとの長さを10センチメートルにそろえた場合の図表示をしてみる。
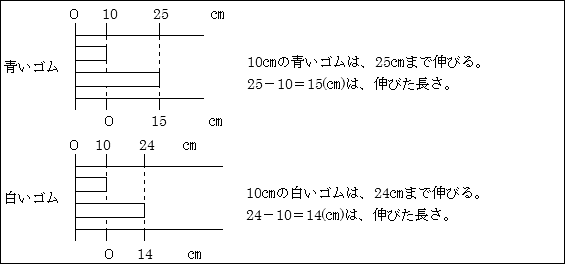
さらにこの方法から、倍の見方で比べる比べ方へと高める指導が必要である。指導の際には、10センチメートルの青いゴムが25センチメートルまで伸びるということは、20センチメートルの場合は50センチメートルまで伸びる…と考え、青いゴムはいつでも2.5倍伸びること、同様に白いゴムは2.4倍伸びることを確認したい。これらの活動の結果、以下のような図表示に表して倍の見方を特徴づけたい。
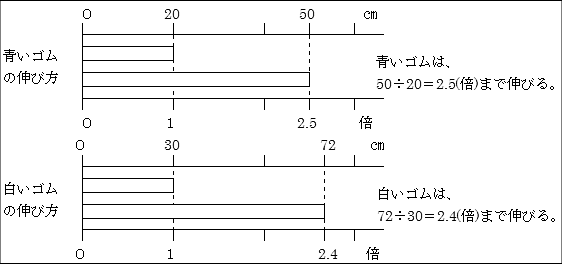
ゴムの伸びで導入するよさは、以下の2つの点である。
![]() 帯小数倍の比較から導入できる。
帯小数倍の比較から導入できる。
小数倍の指導と関連付けた場合、帯小数倍の比較から導入できる点がよい。これは本専門家会議のメンバーからも指摘されていることでもある。
![]() 比例関係を前提としていることがわかりやすい。
比例関係を前提としていることがわかりやすい。
白いゴムは、もとの長さと伸ばした長さに比例関係が内在している。また、差で比較することと倍で比較することを対比した場合、それぞれの比べ方の特徴がわかりやすい。
4.第6学年-単位量当たりの考え、速さ
(1)「単位量あたりの考え」教科書記述の分析
 「単位量当たりの考え」の導入場面での扱われ方
「単位量当たりの考え」の導入場面での扱われ方
教科書では、A社はバンガローのこみぐあい、B社は部屋のこみぐあい、C社はマットのこみぐあいと、3社とも「単位量当たりの考え」の導入では、こみぐあいを場面として扱っている。取り上げている数値は、次の通りである。
〔A社〕
| A | B | C | |
|---|---|---|---|
| 面積 | 16平方メートル | 16平方メートル | 15平方メートル |
| 人数 | 6人 | 5人 | 5人 |
〔B社〕
| A室 | B室 | C室 | |
|---|---|---|---|
| たたみの数 | 10まい | 10まい | 8まい |
| 子どもの数 | 6人 | 5人 | 5人 |
〔C社〕
| あ | い | う | |
|---|---|---|---|
| マットの数 | 2枚 | 3枚 | 3枚 |
| 人数 | 12人 | 12人 | 15人 |
「単位量当たりの考え」で扱う数量には、実際は分布に疎密のあるものでも均等分布しているものと考えていく量が多い。そこで、3社とも、こみぐあいのように、視覚化できる量を「単位量当たりの考え」の導入時に取り上げ、平均の学習と関連させるとともに、こみぐあいを図示させたり、体感させたりするように内容を編成している。そして、児童たちが量の大小比較をするとき、公倍数を用いたり、単位量を求めたりして、2つの量のうち一方をそろえることに気づけるようにしている。このように、こみぐあいのような異種の2量で決まる量の比べ方や表し方を考えていく中で、「単位量当たりの考え」を引き出している。
 考察
考察
例えば、B社の教科書を使用して指導した場合、A室とC室のこみぐあいを比べるとき、差で比べようとしてつまずく児童を見受ける。A室とC室のこみぐあいを比べるとき、1人1枚ずつたたみを使うとして、A室はたたみが4まい、C室はたたみが3まい残る。だから、こんでいるのはC室であると…。また、困ったことに、これは、公倍数を用いたり、単位量当たりを求めたりして計算した答えと一致するので、差で比べる方法も正しいという結論になる。したがって、数値を工夫する必要が生じてくるだろう。
(2)「単位量当たりの考え」提言
次のように数値を変えて児童たちに考えさせてみると、差で比べる方法は可か否か、考えさせることができる。
| A室 | C室 | |
|---|---|---|
| たたみの数 | 8まい | 6まい |
| 子どもの数 | 6人 | 4人 |
A室もC室も残りは2まいなので、こみぐあいは同じと判断する児童がいる。一方、公倍数を用いたり、単位量当たりを求めたりして計算すると、A室がこんでいると考える児童も出てくる。ここで、児童たちの議論が始まる。そして、大抵の場合、A室は残った2まいを6人で使い、C室は残った2まいを4人で使うことになるので、A室の方がこんでいるという結論が導かれる。この過程を、ぜひ教科書の内容に盛り込みたいところである。
また、公倍数を用いたり、単位量当たりを求めたりして計算してもよいことに気づかせるには、次のようにどうすれば同じこみぐあいをつくることができるか、その見方を指導しておくことが大切である。

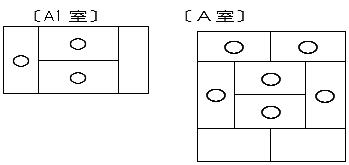
このように図や表を使って、同じこみぐあいをつくるとはどういうことか、考えさせることが大切である。そして、比例の見方が使われていることを、教科書に掲載したいところである。
さらに、単位量当たりを求めておくと、一方の数値を変えてもそれに対する他方の数値をすぐ算出することができるという、単位量当たりのよさに気づけるように教科書の記述を工夫したい。たとえば、A室は「たたみ1まいあたり0.75人」のこみぐあいになるが、それを使うと「たたみ16まいでは12人はいれる」というA室と同じこみぐあいがすぐに算出できることを述べておきたいものである。ここでも比例の見方に着目させたい。
(3)「速さ」教科書記述の分析
 「速さ」の扱われ方
「速さ」の扱われ方
速さは長さと時間という異種の2量で決まる。速さは、長さと時間の2つの量のうち、時間を単位量にとって単位時間に進む長さで表したものである。したがって、速さは、今まで学習した長さやかさなどの量とは異なる。今までのように、単位のいくつ分で測るという考えで導くことができない。
速さには平均や比例の見方が大切である。速さは平均速度を考えるというとらえ方が必要であり、比例関係を仮定して比べていく。したがって、教科書会社3社とも、線分図や数直線図などを用いて、速さについて記述している。
また、速さの公式については、C社が「速さ![]()
![]() 」「道のり
」「道のり![]()
![]() 」「時間
」「時間![]()
![]() 」の3つの公式を掲載している。B社は「速さ
」の3つの公式を掲載している。B社は「速さ![]()
![]() 」「道のり
」「道のり![]()
![]() 」を本文に掲載し、「時間
」を本文に掲載し、「時間![]()
![]() 」についてはキャラクターの吹き出しで小さく掲載している。A社は「速さ
」についてはキャラクターの吹き出しで小さく掲載している。A社は「速さ![]()
![]() 」「道のり
」「道のり![]()
![]() 」の2つを掲載し、時間については、道のりを求める公式を使って、かかる時間を
」の2つを掲載し、時間については、道のりを求める公式を使って、かかる時間を![]() 時間として時間の求め方を考えさせようとしている。
時間として時間の求め方を考えさせようとしている。
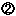 考察
考察
速さの公式を覚えようとする児童は多く見られるが、「速さと道のり、時間」の関数的な関係まで理解しようとしている児童は少ないのが実態である。
B社やC社の記述のように、3つの公式をすべて掲載しておくと、3つともすべて覚えさせるような指導が行われることが少なくない。覚える公式を少なくするためには、「道のり![]() 速さ
速さ![]() 時間」の1つだけでもよいと思われる。その際、式の見方を指導し、あとの2つの公式が導けるようにしたり、関数的な関係に着目できるようにしたりしておきたい。
時間」の1つだけでもよいと思われる。その際、式の見方を指導し、あとの2つの公式が導けるようにしたり、関数的な関係に着目できるようにしたりしておきたい。
(4)「速さ」提言
速さについては、今以上に、速さを数直線や図、表を用いてとらえやすくする記述の工夫が大切であると思われる。実際には、公式化までの過程を丁寧に扱ったり、公式の適用の仕方を身につけさせたりしていきたいものである。たとえば、3キロメートルを15分で進む速さを求めるために、次のような数直線図を用いていけるようにする。
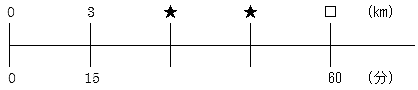
![]() の数の求め方を考えさせ、合わせて
の数の求め方を考えさせ、合わせて![]() 印のところを求めさせながら、時間と道のりの関係を関数的にとらえさせていく。つまり、「3キロメートルを15分で進む速さ」と「6キロメートルを30分で進む速さ」「9キロメートルを45分で進む速さ」などが同じであり、時間が2倍、3倍…になれば、道のりも2倍、3倍…になることに数直線図を通して気づかせていけるようにする。そして、「道のり
印のところを求めさせながら、時間と道のりの関係を関数的にとらえさせていく。つまり、「3キロメートルを15分で進む速さ」と「6キロメートルを30分で進む速さ」「9キロメートルを45分で進む速さ」などが同じであり、時間が2倍、3倍…になれば、道のりも2倍、3倍…になることに数直線図を通して気づかせていけるようにする。そして、「道のり![]() 速さ
速さ![]() 時間」という式は単位時間に進む道のりを何倍かしたものという比例の見方と関連させて扱っていけるように、教科書の記述を工夫したいものである。
時間」という式は単位時間に進む道のりを何倍かしたものという比例の見方と関連させて扱っていけるように、教科書の記述を工夫したいものである。
このような記述がなされることにより、児童たちの比例の見方が育まれるものと思われる。
(田端 輝彦 青山 泰浩 八木 陽)
-- 登録:平成21年以前 --