- 現在位置
- トップ > 教育 > 小学校、中学校、高等学校 > 教科書 > 教科書の改善・充実に関する研究報告書について > 教科書の改善・充実に関する研究報告書(算数)-平成18、19年度文部科学省委嘱事業「教科書の改善・充実に関する研究事業」- > 第1章 5.「数と計算」領域における教科書記述の研究
第1章 5.「数と計算」領域における教科書記述の研究
「数と計算」領域における教科書記述の研究として実施した、ワーキンググループの報告内容は以下の通りである。
「数と計算」領域における教科書記述の研究として実施した、ワーキンググループでは、研究の対象として、小数、分数及び四則計算に注目した。
研究の内容としては、「練習の数量問題」、「導入の重要性への対応の問題」、「文章記述の問題」、「つまずきへの対応問題」の4点について研究した。
以下に、4点の研究内容を整理した。
1.練習の数量問題
計算問題や文章題の数、練習問題の多様性が不足しているとの指摘が教員アンケートに見受けられたが、どの程度の範囲や量を想定しての指摘であるかが不明である。
そこで、「(1)練習問題の数量に関する比較」と「(2)練習問題の多様性についての比較」についての2点からこれを調べていくこととする。すべての学年の比較をすることは難しいのでいくつかの例を挙げて示す。
(1)練習問題の数量に関する比較
 計算問題の量
計算問題の量
教科書における計算練習問題(文章問題による適用題も含む)は
- ア)学習した直後の練習問題
- イ)小単元毎の練習問題
- ウ)大単元毎の練習問題
- エ)数単元毎に適宜扱われる復習問題
- オ)巻末にまとめられている練習問題
- カ)補充・発展内容で扱われている計算練習問題
など、様々な形式・形態で取り扱われている。
例として、5年小数の乗除に関する練習問題の3社における取扱いについて比較する。
小数![]() 整数、小数
整数、小数![]() 整数、小数
整数、小数![]() 小数、小数
小数、小数![]() 小数の計算練習の数量を以下の図表1-13に示した。この中には文章による適用題も含んでいる。
小数の計算練習の数量を以下の図表1-13に示した。この中には文章による適用題も含んでいる。
項の左側が平成12年度、右側が17年度版使用教科書である。
平成12年度版使用教科書は4年で小数![]() 整数、小数
整数、小数![]() 整数、を扱っている。
整数、を扱っている。
なお、「カ)補充・発展内容で扱われている計算練習問題」は除外した。
図表1-13 5年小数の乗除に関する練習問題の3社における取扱いについて
| 計算練習問題数(題) | A社 | B社 | C社 | |||
|---|---|---|---|---|---|---|
| 平成12年度版 | 平成17年度版 | 平成12年度版 | 平成17年度版 | 平成12年度版 | 平成17年度版 | |
| ア)学習した直後の練習問題 | 99 | 127 | 157 | 113 | - | 95 |
| イ)小単元毎の練習問題 | 49 | 101 | 92 | 84 | - | 60 |
| ウ)大単元毎の練習問題 | 36 | 31 | 38 | 44 | - | 27 |
| エ)数単元毎に適宜扱われる復習問題 | 67 | 52 | 81 | 68 | - | 24 |
| オ)巻末にまとめられている練習問題 | 102 | 224 | 34 | 98 | - | 74 |
| 計 | 353 | 535 | 402 | 407 | - | 280 |
C社の平成12年度版については分析時に資料が無かったため割愛
これらの量が絶対的に不足している量であるのか、十分満ち足りている量であるのかは別途研究の余地があり、ここでは判断できない。
また、練習問題の数量が減ってきているかどうかは、2社の比較からは明確に判明しなかった。少なくとも2社の問題数は同じか増加にある。
平成12年度版使用教科書では第4学年から小数の乗除が入っており、小数の乗除を取り扱う期間とページ数の配分から考えると、全体的に以前の方が数量が少ないともいえる。
また、巻末の計算練習がない教科書があったり、数単元毎にある復習問題の中でも全く扱われない期間もあったり、技能の習熟が一様になされている状況とは言い難い面も見られた。
そこで、過去の教科書との計算練習問題数の比較を行った。昭和45年度からおよそ10年毎の比較である。ただし、B社1社の教科書だけの比較である。
図表1-14 B社における計算練習問題数について
| 計算練習問題数(題) | B社 | ||||
|---|---|---|---|---|---|
| 昭和45年度版 | 昭和55年度版 | 平成4年度版 | 平成12年度版 | 平成17年度版 | |
| ア)学習した直後の練習問題 | 306 | 204 | 198 | 157 | 113 |
| イ)小単元毎の練習問題 | 122 | 108 | 115 | 92 | 84 |
| ウ)大単元毎の練習問題 | 73 | 0 | 0 | 38 | 44 |
| エ)数単元毎に適宜扱われる復習問題 | 89 | 147 | 109 | 81 | 68 |
| オ)巻末にまとめられている練習問題 | 10 | 138 | 102 | 34 | 98 |
| 計 | 600 | 597 | 524 | 402 | 407 |
教科書の編集方針や学習指導要領の傾向を配慮しなければならないが、単純に数値の上では、約35年の間に計算問題数は2/3に減少しているといえよう。
 練習ページの量
練習ページの量
平成10年告示の学習指導要領改訂では内容の3割削減及び授業時間数の10~15パーセント減に伴い、平成12年版使用教科書から平成14年版使用教科書のページ数は各社共に平均10~12パーセント減となった。
しかし現在では、むしろ平成17年度版の教科書の方が平成12年度版よりもページ数が多くなっている。したがって、総ページ数に対する練習問題数の割合はむしろ少なくなっているといえる。
図表1-15 3社のページ数について
| A社 | B社 | C社 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 平成12年版 | 平成14年版 | 平成17年版 | 平成12年版 | 平成14年版 | 平成17年版 | 平成12年版 | 平成14年版 | 平成17年版 | |
| 1年 | 112 | 106 | 116 | 108 | 102 | 133 | 112 | 106 | 128 |
| 2年上 | 72 | 74 | 86 | 76 | 72 | 101 | 76 | 76 | 96 |
| 2年下 | 80 | 68 | 76 | 72 | 68 | 95 | 72 | 72 | 92 |
| 3年上 | 86 | 86 | 92 | 84 | 76 | 101 | 92 | 84 | 108 |
| 3年下 | 80 | 68 | 84 | 80 | 72 | 101 | 72 | 76 | 108 |
| 4年上 | 108 | 76 | 103 | 104 | 80 | 109 | 108 | 90 | 118 |
| 4年下 | 100 | 80 | 89 | 100 | 76 | 89 | 106 | 76 | 106 |
| 5年上 | 96 | 98 | 114 | 104 | 96 | 111 | 110 | 96 | 124 |
| 5年下 | 104 | 84 | 92 | 96 | 84 | 93 | 96 | 84 | 100 |
| 6年上 | 100 | 96 | 104 | 104 | 96 | 107 | 108 | 94 | 110 |
| 6年下 | 96 | 88 | 104 | 100 | 84 | 109 | 96 | 84 | 108 |
| 合計 | 1,034 | 924 | 1,060 | 1,028 | 906 | 1,149 | 1,048 | 938 | 1,198 |
練習問題・復習問題のページ数は、5年だけ比較すると以下のようになる。
図表1-16 3社の練習・復習問題のページ数について
| 5年教科書(頁) | A社 | B社 | C社 | |||
|---|---|---|---|---|---|---|
| 12年版 | 17年版 | 12年版 | 17年版 | 12年版 | 17年版 | |
| 練習・復習問題ページ | 38 | 36 | 44 | 38 | - | 42 |
| 総ページ | 200 | 206 | 200 | 204 | 206 | 224 |
| 練習問題配置率 | 19パーセント | 17.5パーセント | 22パーセント | 18.6パーセント | - | 18.8パーセント |
総ページ数が増えたものの練習・復習問題ページは増えていないため、全体の割合としては減っている。
 提言
提言
これらを受けて、改善の方向としては以下の4点が挙げられる。
- 巻末の計算練習問題は、授業や家庭学習において、適宜練習できるよう配置しておくことが望ましい。
- 小数の乗除のような重要な計算練習は、随時復習問題等でチェックさせると共に、継続的に習熟を図っていくようにする。
- 教科書以外のワーク・ドリル等の使用が通常化していることを考えると、教科書で十分な練習問題のページを確保しておく必要がある。しかし、それが児童や教員にとって「やらなければならないもの」「終わらせなければならないもの」という義務感や責任感としてプレッシャーがかからないように配慮する必要がある。
- 数と計算の練習問題では、とかく計算練習に終始しがちであるが、演算決定の問題も練習に加えていく必要がある。これは文章問題を解くことと同じであるが、できれば演算決定だけを取り扱う問題があってもよい。
(2)練習問題の多様性についての比較
 練習問題の示し方
練習問題の示し方
練習問題の多様性といった場合、具体的にどのような種類のものを想定しているのかが不明である。
ここでは、練習問題の提示の仕方について分析をしてみる。
練習問題の示し方は
- ア)横書きの計算や縦書きの計算が羅列されている、いわゆる計算問題
- イ)ゲーム化やパズル化した計算問題
- ウ)文章だけで示された、いわゆる文章問題
- エ)さし絵や表、図などの情報が文章と共に示されていて、必要な情報を選択して解く問題
などが現在の教科書に主に見られる。
そこで、上記イ)とエ)の観点で示されている箇所が練習、復習、まとめ(評価)の各ページの中にいくつあるか、を調べることとした。(5年の数と計算領域だけに限る)
図表1-17 練習問題の示し方について
| A社 | B社 | C社 | |
|---|---|---|---|
| イ)ゲーム化やパズル化した計算問題 | 7(注1) | 6(注2) | 4(注3) |
| エ)必要な情報を選択して解く問題 | 0 | 1(注4) | 0 |
ア)やウ)などはこれまでの教科書における典型的な練習問題スタイルであった。最近の教科書にはイ)やエ)などの工夫された問題が示されているが、数が少なく、まだまだ児童の自発的な挑戦意欲や習熟努力を促すような内容であるとはいえない。
さらに、発展的な取扱いのページには魔方陣(A社)や平方根(C社)などを使った小数の計算練習などが見られた。しかし、発展的な取扱いによるこのページは授業時間数にカウントされていないことや全員の児童がチャレンジする内容ではないことを考えると、一部の児童が取り組む程度の扱いとなる。
- (注1)A社5年上巻及び下巻に見られる計算練習は、計算の結果を組み合わせて文章を作る形式のもの。
- (注2)B社5年上巻及び下巻に見られる計算練習は、計算の結果をたどって進む迷路型の形式のもの。
- (注3)C社5年上巻及び下巻に見られる計算練習は、計算結果を組み合わせて文章や文字を作ったり迷路を進む形式のもの。
- (注4)B社5年上巻の問題は、情報を選択して求める文章問題。
 練習問題の質
練習問題の質
一般に単純な縦書き、横書きの計算練習問題は、2項の計算によるものがすべてである。文章による問題も、その多くは2要素の関係から2項の計算で求めていく場合が多い。文章問題の中には、3要素2段階で考えを進める問題もある。
これも、まず2要素の関係を明らかにして2項の計算で求め、その求められた1項と残りの1要素とを組み合わせて、2項の計算で求めることになる。したがって、3項の計算は2項の計算ができれば十分である。こうした考えが教科書各社にみられる。
芳沢委員は、「算数・数学が得意になる本」(注5)の中で、3項計算の必要性や重要性について述べている。とりわけ、計算法則を誤って理解したり使ったりする原因の一つとして、小学校における3項の計算練習問題がほとんど扱われていないことにあると指摘している。
実際の社会の中で用いられる場面は少ないものの、算数・数学を直接的に活用していく仕事や学問、高等数学を学んでいく場面では、多項計算がもっとも多く使われることになる。
日常卑近な場面で使用する計算だけでなく、中学校や高等学校における高等数学を見据えた計算練習を、簡単な数値で処理のできる小学校の算数で取り組んでおくことも配慮する必要がある。
- (注5)「算数・数学が得意になる本(講談社現代新書:芳沢光雄著)」より
 提言
提言
これらを受けて、改善の方向としては以下の4点が挙げられる。
- 練習問題の与え方としては、各教科書ともア)やウ)などの従来の形式的なものしか用意されていない。イ)やエ)などの工夫した問題の与え方を考慮する必要がある。
- 特に、情報を自ら選択して問題の解決に当たることが、これから望まれることを考えると、文章だけの、いわゆる文章題だけでない問題の与え方を工夫する必要がある。
- 単純に数値を組み合わせるだけでなく、過剰条件や条件不足、また条件を自ら変えてみるなどの問題も検討し、工夫して取り入れていくことも必要である。
- 3項の計算練習問題を、適宜取り入れていく必要がある。
2.導入の重要性への対応の問題
教科書では、単元(小単元も含む)の導入場面に様々な工夫がなされている。
教員アンケートの意見の中には、導入場面での工夫が児童の意識を単元の学習内容に向けさせ、導入をスムーズにしているとの指摘が見られる。
一方では、今の教科書構成では学習の導入部分が不足しているといった指摘もある。
これらの意見を踏まえ、「数と計算」領域の中でも、特に、小数や分数の扱いに焦点を絞って、望ましい導入のあり方について検討し、提言していきたい。
教科書の導入場面には、次のようなページ構成や問題設定の工夫が見られる。
- (1)既習事項の確認と新たな学習課題の設定
- (2)身の回りで使われている数の紹介(実生活との結びつき)
- (3)数範囲を拡張していけるような場面設定
- (4)児童が計算の仕方を考えていくときのイメージに結びつく場面設定
以下、現行の教科書から、その具体例を示しながら、意見を述べさせていただく。
(1)既習事項の確認と新たな学習課題の設定
 考察
考察
単元に入る前に、基礎となる既習事項の確認を行うことにより、既習の内容を思い出させるようなページを設けている。
C社では、「思い出してみよう」がそれに当たる。例えば、5年の「分数」の前(5年下)には、「![]() 1メートルを5こに等しく分けた1こ分の長さ」「
1メートルを5こに等しく分けた1こ分の長さ」「![]() 5こ分で1メートルになるはしたの長さ」などを分数で答える問題3題と、図で表された液体の量やテープの長さを仮分数と帯分数で答える問題がある。ここで、4年の「分数」で学習した内容の確認が行われる。
5こ分で1メートルになるはしたの長さ」などを分数で答える問題3題と、図で表された液体の量やテープの長さを仮分数と帯分数で答える問題がある。ここで、4年の「分数」で学習した内容の確認が行われる。
A社では、「分数と小数」の単元の前(5年下)に、「わり算と小数、分数の関係をふりかえろう」という問題が4問設定されている。ここには、C社のような問題に加えて、2本のテープの倍関係を答える問題や、簡単な場合について分数と小数を対応させる問題が掲載されている。
いずれも、穴埋め式のごく簡単な問題であるが、一通りなぞることによって、新しい単元の学習に直結する内容を思い出すことができるように配慮されている。
さらに、新しい学習課題を見出すことをねらったものを取り上げている場合もある。
例えば、6年の「分数のかけ算とわり算」の単元の前では、図表1-18ような表にこれまでに学習した計算を整理することによって、分数のかけ算とわり算が未習であることをとらえさせ、新たな課題としてスムーズに進んでいけるようにしてある教科書もある(C社は6年下、A社は6年上。表はA社のもの)。
図表1-18 かけ算とわり算の示し方について
| 整数 | ||||
|---|---|---|---|---|
| 小数 | ||||
| 分数 |
 提言
提言
数範囲を広げたり、新しい計算について考えたりしていくときには、既習の内容や考え方を基にする。ところが、関連する内容を学習してから長い時間がたってしまうと、児童は、以前学習した意味や用語を忘れてしまっていることが多い。よって、このような振り返りのページを設けることは、児童のスタートラインをある程度そろえるためにも、有効に機能していると思われる。
紙面としては1ページ程度だが、単元と単元のつながりを見据え、実態に合ったページ作りをしていくことが望まれる。
このページを丁寧に扱いすぎると、単元の内容に入らないまま1時間の授業が終わってしまうこともあるようだ。前に学習した内容の振り返りは、新しい内容を学習しながらでもできる。復習に時間が取られ過ぎることのないように、このページの扱い方を、指導書等で示していくことも必要である。
(2)身の回りで使われている数の紹介(実生活との結びつき)
 考察
考察
数は、日常生活の様々な場面で使われている。児童たちも、例えば、大きな数については、品物の金額とかニュースの中で使われているのを耳にしているはずだし、小数は身体測定や徒競走のタイム、温度、食料品の重さやかさなどで使われているのを知っている。身の回りで使われているこれらの数を、単元に入る前に紹介してあげることにより、より身近に感じ、あまり抵抗なく学習に取り組めるものと考えられる。
「小数」と「分数」は、4年で初めて登場する。A社、B社の教科書を見ると、この単元の前に、「こんな数、見たこと(が)あるかな?」というタイトルのページ(A社4年上。B社4年上と4年下)がある。そこには、日常生活の中で使われている小数や分数の写真がたくさん掲載されている。
 提言
提言
身の回りで使われている数を見て、小数や分数がわかったつもりになる児童がいるとしたら逆効果である。小数について言えば、はしたを数値化するために、「1デシリットルを10等分して小さな目盛りをつけよう」というようなアイデアを児童から引き出し、「その1目盛り分が0.1デシリットルである」というように、十進位取り記数法についての指導がきちんとなされる単元構成になっていることが前提であることは言うまでもない。
身の回りで使われている数を例示する場合、その数が何を表しているのかが、学習後にわかるものが望ましい。
B社の教科書では分数の写真を例示しているが、そこでの分数は割合として使われているもの(例:油の汚れが1/10、塩分1/2)である。これは、4年で学習する分数とは表しているものが異なる。そのため、児童にはその意味の理解が難しいと思われる。例示するのであれば、学習した事柄と関連付けてとらえられるものがよい。
数への感覚を豊かにするために、数の大きさを感覚的にとらえさせるための例示があるとよい。A社の「小数」の前のページ(A社4年上)には、「1リットル」「0.8リットル」「1.2リットル」の水筒が並べて示されている。この写真から、1と0.8と1.2が表す大きさの違いを、(正確にではないが)感じ取ることができる。この例の他にも、視覚的に1と0.1が比較できるような具体的な写真とか、数の大きさ(小ささ)を実感できるような読み物などを、導入場面に限らず(単元の途中や終わりにも)適宜盛り込んでいけるとよい。
(3)数範囲を拡張していけるような場面設定
 考察
考察
「整数![]() 整数」→「小数
整数」→「小数![]() 整数」→「整数
整数」→「整数![]() 小数」→「小数
小数」→「小数![]() 小数」のように、使える数範囲を少しずつ広げて考えていくことができるように場面が設定されている。
小数」のように、使える数範囲を少しずつ広げて考えていくことができるように場面が設定されている。
例えば、C社の「小数のかけ算」では、次のような問題が提示されている。
「![]() リットルずつ入っているジュースのびんが、3本あります。ジュースは全部で何リットルあるでしょうか」
リットルずつ入っているジュースのびんが、3本あります。ジュースは全部で何リットルあるでしょうか」
この問題では、まず![]() の中が整数の場合(「2リットルとすると…」「3リットルとすると…」)を考える。次に、
の中が整数の場合(「2リットルとすると…」「3リットルとすると…」)を考える。次に、![]() の中に小数を入れてみる(「1.2リットルとすると…」)。このようにして、小数
の中に小数を入れてみる(「1.2リットルとすると…」)。このようにして、小数![]() 整数の計算の仕方を考えていくわけである。
整数の計算の仕方を考えていくわけである。
同じようにして、数範囲を広げながら、かけ算の意味の拡張をしていく。このような単元構成は、どの教科書でも行われている。
 提言
提言
このような問題場面の設定や展開の仕方は、これまでも考えられてきたものであるが、次のような点について、さらに検討を重ねていく必要がある。
- どのような数値がよいか。
- どのような場面設定がよいか(具体的にイメージして考えやすいか。)。
- 数直線などを使って考えさせることが多いが、それが本当に児童の思考に合ったものになっているか。
(4)児童が計算の仕方を考えていくときのイメージに結びつく場面設定
 考察
考察
教科書の文章題では、計算の仕方を考えるときに、図に表したり具体物を操作したりしやすいような場面設定がなされている。
例えば、「分数のかけ算とわり算」の導入では、A社、B社、C社とも、ペンキ塗りの場面の問題が扱われている。同じような場面設定になっている理由は、分数のかけ算やわり算は、面積図を使うと説明がしやすいと考えられているためである。
 提言
提言
児童にとって具体的な場面をイメージしやすく、モデル化しやすい場面を扱うことは、児童の思考を助けるものであるから、今後もよりわかりやすい場面設定を心がけていただきたい。
「分数のかけ算とわり算」を例に挙げたが、ペンキ塗りの場面が本当に児童の思考に合っているかどうか、再検討が必要である。例えば、4/5![]() 2の計算は1/5を単位として見ると、4
2の計算は1/5を単位として見ると、4![]() 2の計算と同じと考えることができる。
2の計算と同じと考えることができる。
導入における、新しい場面設定の開発を期待したい。
3.文章記述の問題
記述について、「イラスト・吹き出し」、「![]() などの記入欄」、「全体的な記述」の3つの視点で問題点を明らかに、改善の提言を行う。
などの記入欄」、「全体的な記述」の3つの視点で問題点を明らかに、改善の提言を行う。
はじめに、記述について全般的な立場で問題点を述べ、それを受け、数と計算分野についての改善点を述べる。
(1)記述についての状況(教員・保護者アンケートから)
 アンケート結果から
アンケート結果から
a.吹き出しが掲載されていることについて
ア)吹き出しについての教員アンケート結果
- 88.7パーセントの教員が効果的にもちいられていると回答している。
効果的:18.8パーセント まあ効果的:69.9パーセント - 自由記述の回答から
書き込みのしやすさやイラスト、ヒントが学習を助けている。
(教員、保護者)
イ)効果的でないと回答した教員の理由
- 不必要なものが多い:44.7パーセント
- 自由記述の回答から
過剰なまでのイラストは子どもの数学的感覚を養うことを阻むのではないか(保護者)
イラストや写真、吹き出しが多すぎるという印象であまりにも親切過ぎる(保護者)
文字離れを助長させるのではないか(保護者)
ヒントや考え方が書きすぎており、教科書を使った指導が難しい。(教員)
自分で考える力を伸ばすためにイラストや図解を控えめにする。(教員)
b.記入欄の活用について
- 活用している:83.6パーセント
- 自由記述の回答から
書き込みスペースが小さい(保護者)
c.全体的な記述について
- 自由記述の回答から
説明の丁寧さが自由な思考の妨げになっていることについて配慮した活用が足りない(教員)
 教員アンケート結果のまとめ
教員アンケート結果のまとめ
イラストや吹き出しについての効果があると多くの教員が認めている。
反面、数学的感覚や思考力を育てるためには、丁寧すぎないかといった指摘がある。イラストや吹き出しが効果的に活用されているかどうかは不明確である。
![]() などの記入欄については、活用している教員が多いが、効果的な活用がなされているかどうかについては不明確である。
などの記入欄については、活用している教員が多いが、効果的な活用がなされているかどうかについては不明確である。
(2)数と計算分野の記述の問題点
 イラストや吹き出しについての問題点
イラストや吹き出しについての問題点
a.吹き出しのパターン
- 解決のヒントとなる吹き出し
「
 すると・・・」型 「
すると・・・」型 「
 だよ」型 「
だよ」型 「
 かな」型
かな」型 - 学習の指示となる吹き出し
「
 をやってみよう」
をやってみよう」 - 説明をしている吹き出し
「
 となる」
となる」 - キャラクターの対話型による提示
「
 して考えると・・・」「
して考えると・・・」「
 して考えると・・・」
して考えると・・・」
b.事例
図表1-19 事例1 4年小数のたし算の紙面にみられる吹き出しの状況
| A社 | B社 | C社 |
|---|---|---|
| 吹き出し回数 1 | 吹き出し回数 2 | 吹き出し回数 1 |
|
|
|
| 説明型の吹き出しである。 | 説明型と解決のヒント型の2つ吹き出しを併記している | 解決のヒント型の吹き出しである。 |
図表1-20 事例2 6年分数のたし算
| A社 | B社 | C社 |
|---|---|---|
| 吹き出し回数0 | 吹き出し回数1 | 吹き出し回数5 |
|
|
|
これまでの分数の学習を復習( ↓ 簡易な場合の分数のたし算 ↓ 等しい分数 ↓ 通分 ↓ 分数のたし算 ↓ 約分 |
分数の数直線で復習 ↓ 等しい分数 ↓ 約分 ↓ 通分 ↓ 異分母たし算 |
等しい分数で復習 ↓ 分数の大小 ( ↓ 通分 ↓ 約分 ↓ 異分母たし算 |
c.事例1、2からみる問題点
- 教科書の作成意図により、吹き出しが異なる。
- 事例1 4年「小数のたし算」の場合、B社については、ていねいすぎないか。授業者がどの様に扱うのか不明である。2つの吹き出しをみたとき、児童が混乱しないか。
- 事例2 C社6年「分数のたし算」の場合、ヒント型の吹き出しが多く、ていねいであるが、自ら考えたり、思考力を伸ばしたりすることに弊害はないか。
(3)全体的な記述についての問題点
 教員の主発問に関する記述
教員の主発問に関する記述
教員は、教科書に書かれた記述や問題をもとにして、授業計画をたてる。教科書を見て、教員の指導計画の視点としては、主に次のことがある。
- ア)今日の学習内容は何か
- イ)課題は何か
- ウ)1時間でどこまで扱えばいいのか
- エ)主発問はどうしたらいいのか
- オ)教える(説明)ことは何か
- カ)練習問題にどんな問題があるか
ア)~カ)は、算数を専門的に教えている教員ではなく、一般的な教員を念頭にしている。
ア)~オ)が、教科書で明確にわかるようになっていると、教員は授業計画をたてやすい。そのことが児童にとってわかりやすい授業につながる。
ア)~カ)の中で、特にエの記述が下の事例のように、明確になっていない場合がある。
a.事例
図表1-21 事例3 4年 小数 第1次
| A社 | B社 | C社 |
|---|---|---|
| 「はしたの大きさの表し方を考えていこう」 | 「はしたの大きさの表し方を調べよう」 | 「はしたを数で表す方法を調べよう」 |
図表1-22 事例4 4年 小数のしくみ(小数を数直線で表すこと)
| A社 | B社 | C社 |
|---|---|---|
| 小数のしくみ | 小数の大きさ | 小数のしくみ |
| 主発問に関する記述がある。 「小数を数直線に表しましょう」 |
主発問に関する記述はない すぐに課題(問題)が提示されている |
主発問に近い記述になっている 2小数のしくみ 「1 下の図で調べましょう」 |
| 課題 (数直線が示してあり、図中にア、イ、ウの印がある) ア、イのめもりは、それぞれどんな大きさを表していますか。 |
課題 2.6は、1を何こと0.1を何こあわせた数ですか。また、2.6は、0.1を何こ集めた数ですか。 |
課題 (数直線が示してあり、図中に、あ、い、う、え、おの印がある) ↑の表している小数を書きましょう。 |
b.事例3、4からみる問題点
- 小数第1次については、教員の主発問にあたる記述が各社なされているが、第2次「小数のしくみ」では、主発問にあたる記述が不明確になっている。
A社は、教員は「今日の勉強は小数を数直線に表しましょう」と主発問の参考にすることができる。
B社は、教員が「小数の大きさを勉強しましょう」と補足することになる。ただし課題(問題)との結びつきが学習者に明確になるか問題である。
C社は「今日は小数のしくみを学習します。下の図で調べましょう」と主発問の参考にすることができる。
 記入欄の設定についての問題点
記入欄の設定についての問題点
a.記入欄のパターン
![]() にしているパターンや下線がひいてあるパターンがある。
にしているパターンや下線がひいてあるパターンがある。![]() のパターンが多い。
のパターンが多い。
b.事例
図表1-23 事例5 4年小数のたし算
| A社 | B社 | C社 |
|---|---|---|
| 記述欄 1 | 記述欄 |
記述欄 なし |
| 課題 0.5 式 となっていて、式をかかせる記述欄がある |
課題 0.6 式 0.6 |
課題 0.4 式は、0.4 |
図表1-24 事例6 6年分数のたし算
| A社 | B社 | C社 |
|---|---|---|
| 記述欄 |
記述欄 |
記述欄 |
通分した場合の分子を <なおこさんの考え> <まことさんの考え> |
式
|
通分した場合の分子を
|
c.事例5、6からみる問題点
- B社では、課題となる式(分数をたす式)と答えを書かせるようにしている。A社とC社では、通分した際の分子を書かせるようしている。
- B社の場合、授業の流れの中でどの時点で、課題の式(分数をたす式)を書かせるかを教員が計画しておく必要がある。(通常は、課題を与えた後に分数をたす式を記入させるが、場合によっては、授業の終末で記入しながらまとめる場合もある)また、紙面を見ても
 が多いため、学習することが一見するとわかりにくい。
が多いため、学習することが一見するとわかりにくい。
(4)数と計算分野の記述の改善点
 吹き出しの扱いについて
吹き出しの扱いについて
a.提言
吹き出しについては、前述で示した問題点のように、吹き出しの記載数が多い場合があった。特に、ヒント型の吹き出しが多く、思考力の育成で問題となる場合も考えられる。
そこで、吹き出しについては、その効果を認めながら、教員と学習者が煩雑とならないように、必要なものに精選する。また、数学的な見方・考え方を育成する立場にたち、ヒント型の吹き出し記述を中心とする。
b.吹き出しの改善点
吹き出しの掲載数
- 必要なものに精選する。
- 吹き出しに書いてある内容は、教員が必ず扱うとは限らない。吹き出しが多いと教員は、どれを活用するのか不明になる場合がある。
- 教員には、本文に書いてあることは必ず扱わなくてはいけないという意識がある。そこで、吹き出しの記述で説明型のもので必要なものは本文に書くとよい。
吹き出しの記述内容
- 記述内容が、ヒント型、説明型、指示型といくつかのパターンがあったが、煩雑であるために、ヒント型を中心に掲載する。
- ヒント型の吹き出しについては、数学的な見方・考え方を育成する立場にたったものにする。
- 全学年に共通した立場にたち、スパイラル的に記載していく。
- 指導側の立場にたち、吹き出しの内容を教員の補助発問として使えるようにする。この立場にたつと、ヒント型で「

 とすると…」「
とすると…」「
 かな」といった、その児童の考えを引き出すパターンの記述が望ましい。
かな」といった、その児童の考えを引き出すパターンの記述が望ましい。
数と計算領域における吹き出しの記述の例
- スパイラル的に掲載し、数学的な見方・考え方を育てる
- ア)単位の考えにたった記述
「
 をもとにして考えると…」
をもとにして考えると…」
4年小数「0.1をもとにして考えると…」
6年分数のたし算「分母が同じときはたし算ができたから…」 - イ)計算の統一性に関する記述
「
 の計算と同じと考えると…(考えられないかな)」
の計算と同じと考えると…(考えられないかな)」
5年小数のかけ算「整数の場合と同じように考えると…(考えられないかな)」 - ウ)計算の決まりに関した記述
「
 算の場合は
算の場合は
 できたから…」
できたから…」
6年分数の割り算「わり算では、割られる数と割る数に同じ数をかけてもよかったから…」
5年整数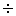 小数「わり算のきまりが使えないかな」
小数「わり算のきまりが使えないかな」
- ア)単位の考えにたった記述
 全体的な記述について
全体的な記述について
a.提言
前述の問題点で示したように、ア~カの視点が明確にわかるようになっていると、教員は教科書を見て指導計画をたてやすい。特に、教員と学習者が、今日は何を勉強するのか、わかるような記述が必要である。
b.全体的な記述に関する改善点
- 課題を提示する際の教員の主発問に相当する記述をいれる。
- 吹き出しの中で、説明型で扱っているもので重要なものは、本文に記述する。
 記入欄の設定について
記入欄の設定について
a.提言
![]() などの記入欄を設けることは、学習者に記入させることで、理解度を評価するとともに、基礎・基本となる内容の定着を図ることができるという効果がある。前述の問題点で示したように、記入欄があることで授業者はその扱いをどのようにするかにより、授業の流れがしばられることもある。
などの記入欄を設けることは、学習者に記入させることで、理解度を評価するとともに、基礎・基本となる内容の定着を図ることができるという効果がある。前述の問題点で示したように、記入欄があることで授業者はその扱いをどのようにするかにより、授業の流れがしばられることもある。
そこで、記入欄については、目的を、「授業のポイントになる点について、定着を図るとともに、評価できるようにするため」として、多くならないように配慮する。すなわち、記入欄が多いために学習内容が不明確になることを避ける必要がある。
b.記入欄設定に関する改善点
- 記入欄は必要最低限とする。
- 学習の基礎・基本となる点について、ポイントを絞って
 などの記入欄を設ける。
などの記入欄を設ける。
- ア)式をきちんとかくために
 を設定する
を設定する - イ)考え方の定着を図るために
 を設定する。
を設定する。
- ア)式をきちんとかくために
4.つまずきへの対応問題
(1)つまずきへの対応
児童へのアンケートによると、高学年になるにつれて算数への苦手意識が強くなる傾向がある。積み上げ型の教科内容ゆえ一度つまずくと、以後の学習に興味・関心を失ったり、知識・技能が対応していけなかったりなどの問題が生じる。
そこで、つまずきを取り戻すための仕掛けや仕組みを取り入れた教科書の在り方について考える。
つまずきへの対応として、教科書では次の3点が特徴的に示されている。
- ア)新規の内容を学習する前に、それにかかわる既習の内容を復習したり、レディネスチェックしたりするなどの内容が見られる。
- イ)新規の内容を学習している中で、典型的なつまずきを見せるところや、陥りやすいつまずき箇所に対して、キャラクターの吹き出しや学習の方向性を示す指示が見られる。
- ウ)新規の内容を学習した後で、学習内容が確実に理解、定着しているかを自分でチェックする機能が見られる。
これらの対応が十分であるかは、問題の量や内容の質及び取り上げる内容の範囲、また自己評価の仕方などのチェックの方法などの観点から詳しく検討する必要があろう。
しかし、これらの点については教科書会社それぞれの編集方針に基づくものであり、簡単にその良否を述べることはできない。
ここでは、前述のア)~ウ)の内容を各社毎に分類併記し、これからのつまずき対策に必要と思われる内容を提言としていく。
 現行教科書の対応状況
現行教科書の対応状況
図表1-25 つまずきに対する現行教科書の対応
| A社 | B社 | C社 | |
|---|---|---|---|
| 単元導入時の対応 |
|
|
|
| 単元途中での対応 |
|
|
|
| 単元終了後での対応 |
|
|
|
各社とも、表現の違いはあっても、単元導入時、単元途中、単元終了後、それぞれにつまずきへの対策を取っていることが分かる。
単元導入時では、ほぼ同様にレディネスチェックが行われており、児童自身が学習したことを覚えているどうかをチェックすると共に、教員側も授業に入る前の児童の実態を知っておくための情報にもなっている。また、単元の導入時の「プロローグ」や「課題設定」の問題は既習事項から取り組めるような配慮がなされている。
単元途中では、A社は本時の問題を示した後、学習問題の焦点化を図る「学習のめあて」を示しているところが特徴的である。また、B社はどのように問題と取り組んでいくか、考え方の切り口を示したり、どのような考えを使ったのかをまとめたりする「学習のきっかけ」、「学習のまとめ」をキャラクターで示しているところが特徴的である。
単元終了後の対応としては、各社とも練習問題、評価問題、補充問題等できちんとした習熟、定着を図ろうとしている。その中で、B社C社は単元終了後の練習や評価問題の中で、その問題につまずいたときは「![]() ページ」に戻りなさいという「ふりカエル」指示をしていることが特徴である。
ページ」に戻りなさいという「ふりカエル」指示をしていることが特徴である。
 つまずきの記述
つまずきの記述
一つの問題に対して複数の考え方を示してくる記述がいくつかの内容の中に見られた。この場合、ほとんどが正解、もしくは正しい考え方だけが示されるだけで、典型的な間違いやつまずきは教科書に示されていない。例えば、2/3![]() 4/5の計算で、分母・分子をそれぞれ足して6/8とする児童の反応を取り上げることはない。練習問題で「次の計算の間違えを見つけなさい」という内容はA社がよく取り上げているが、本文内容の中では、どこも取り上げていない。
4/5の計算で、分母・分子をそれぞれ足して6/8とする児童の反応を取り上げることはない。練習問題で「次の計算の間違えを見つけなさい」という内容はA社がよく取り上げているが、本文内容の中では、どこも取り上げていない。
教科書に誤った考え方を掲載するのは、現場での指導に混乱を生じさせることにもなる、という教科書作成者側の考えもあるためである。しかし、児童にとって「反面教師的」な取扱いを工夫する必要があると考える。
 提言
提言
つまずきへの対応や振り返り方について、上記のことを踏まえて以下のように提言する。
- 教科書本文中(単元途中)で、多様な考えを記述する場合、つまずきの多い箇所では、不十分な考えや誤った考えも適宜取り上げていく。
- A社のような練習問題における「計算間違い」の修正も、適宜導入しておきたい。
- B社・C社の単元末にある練習や評価問題の中で、つまずいた箇所の本文へのフィードバック指示は指導者にとっても、児童にとっても必要である。ページの指示だけでなく、内容の具体的な指示もあればなおよい。
- 計算などは積み上げ型であるため、ある程度の習熟が必要である。場合によっては直近の既習内容や既習事項だけを示すのではなく、前学年の内容も復習やレディネステストの内容として組み込んでおくことが望ましい。
- 巻末の補充問題も当該学年の計算練習問題だけでなく、下の学年の計算練習問題を掲載しておく配慮も必要であると考える。
(家田 晴行 夏坂 哲志 鈴木 正則)
-- 登録:平成21年以前 --