- 現在位置
- トップ > 教育 > 学校等の施設整備 > 防災への取組 > 学校施設の耐震化推進について > 学校施設の耐震化推進に関する相談窓口 > 専門的・技術的な質問に対する回答(屋内運動場関係) > 専門的・技術的な質問の詳細と回答(屋内運動場関係)
専門的・技術的な質問の詳細と回答(屋内運動場関係)
1.屋内運動場等の耐震性能診断基準に関する質問
(付-2)
No.付2-1
質問
1.「屋内運動場等の耐震性能診断基準」付-2 表A2に記載されている算出方法は節点振分法などの基本式から求められた式でしょうか?式の根拠を教えて下さい。
2.同表(表A2)で、gMs(0.5L)などの「分布荷重」は、想定されているのは、長期荷重で良いでしょうか?
回答
1.節点振分法です。
例えば風下側柱頭の曲げ耐力MⅠにおいては、M1(geMm)は梁端部における梁部材断面の曲げ耐力であり、M2(geMj)は梁端仕口における接合部の曲げ耐力ですので、節点の曲げ耐力はこの2つのうち小さな方の値以下となります。さらに、柱上端部における柱部材断面の曲げ耐力M3(ctMm)、柱上端仕口における接合部の曲げ耐力M4(ctMj)も併せて考えると、節点の曲げ耐力はM1からM4の中で最小の曲げ耐力以下となります。以下、せん断により梁もしくは梁における接合部の曲げ耐力が決まる場合など、端部における部材の曲げ耐力もしくは仕口における接合部の曲げ耐力以外の条件で節点の曲げ耐力が決まる場合も含めて、曲げ耐力の最小値を求めるようになっています。
2.地震力算定用の鉛直荷重です。
(追加質問)
1.上記の質問と同じ表(付2 23ページ)に質問。
M9=cmM + (cmM + cbM)×(H-Hm)/HmのF値ですが、cmM=min(cmMm , cmMj)で決定した方(cmMm又は,
cmMj 小さいほうのF値)でM9のF値を決定すべきでしょうか。
※cbMで決まった方ではないと思いました。
※M10 , M12 , M13 , M19 , M20も同様に考えればよいのか。
2.1と類似ですが
M16=2×(gmMm-gMs(0.5L)) +MⅠ
はgmMmのF値を採用すればよいでしょうか。
3.付3 30ページでM2/M1の値で、(終局メカニズム時の応力状態を仮定する)とあります。付2の方法で検討する場合、具体的には、フレームのヒンジが生じる節点を想定(初期応力状態、耐力から)しますが、終局状態ということで、全節点にヒンジが生じるとして、検討する部材部分端部における長期と終局耐力を加算したもので、M1とM2を決定すると思いますが終局耐力はM2/M1が決定しないと決定しないので、どのように検討したらよいでしょうか。
(追加回答)
1.2.F値の決める原則は「屋内運動場等の耐震性能診断基準(平成18年版)」11ページにあるとおり
「(2)架構の各節点を代表するじん性指標を、節点に集まる部材・接合部のうち、塑性化する可能性のある要素の要素じん性指標とする。節点に集まる部材、接合部等のいずれが塑性化するか特定できない場合、または同時に塑性化する場合には、最小の要素じん性指標を用いる。」となります。
ここでは、節点の耐力を決定づける各数値がどのようにして決まったかを勘案した上で、対応したF値をとってください。
3.付録2で示されているのは「略算法」であり、精解を求めるものではありません。付録3で示されている式は、横座屈耐力の設計式ですが、M2/M1は「仮定」すると書かれています。
最初にM2/M1の値を仮定することから始めてM2/M1の値が精解となるまで計算をやり直すなど、いろいろな方法があるかと思いますが、どのように運用するかは診断者が決めてください。
No.付2-2
質問
屋内運動場等の耐震性能診断基準第2版(平成18年)について質問します。
23ページのMⅠの算定で風下柱頭部のM1~M4で梁の長期応力が考慮されていません。M5~M8で、せん断耐力で決まる曲げ換算には考慮されています。これでは、曲げ耐力として不十分ではないでしょうか。
ちなみに、24ページのA2.2図の曲げモーメント図は梁の曲げモーメントは分布荷重により直線ではなくカーブしているのは正しい性状ですが、前述のように耐力としてこの長期曲げが考慮されない計算結果となっています。
風上のMⅢでは、長期は地震時をキャンセルする方向に働くので梁端より中間でヒンジが発生する可能性があり0.5L、0.25Lでの長期曲げを考慮しているのは正しいと思います。
一般的には、長期を考慮すれば風下柱頭で曲げが最大となります。特に体育館のような大スパンでは顕著です。
風下柱頭で梁端部の長期曲げ応力を考慮しない理由をご教示ください。
回答
ここで示されている方法は略算法です。中間荷重(長期応力)の影響については、両端をピンとした単純梁として算定した上で考慮しています。そのため、M1~M4では中間荷重の影響は0となり、一見考慮していないように見えるだけです。
(追加質問)
『両端をピンとした単純梁として算定した上で考慮しています。そのため、M1~M4では中間荷重の影響は0となり、一見考慮していないように見えるだけです。』
私なりに再考したところ、ご回答では少々不十分ではないかと思いました。
つまり、M1~M4で考慮されていないのは、この計算法が極限解析で接合部等のヒンジを許容しており結局のところ、風上と風下の柱せん断力の合計で長期のMを相殺するため考慮の必要がない、ということだと思います。
ただし、梁にとっては中間部においては相殺するものがないので長期を単純梁応力にて考慮している、ということだと思います。(M16~M17)梁端部のせん断力についても同様です(M5~M6)つまり、両端をピンとした単純梁として算定したから柱頭への影響が0となるわけではないと思います。
(追加回答)
図2の応力状態について、風上と風下の合計で長期荷重によるモーメントの影響を相殺することで図4 のように考えるべきではないかということですが、回答では、図1 に示しました長期荷重による応力分布を、最終的に風上と風下で相殺されるということで材端の固定度の影響を無視し、単純梁(両端ピン)を仮定した図5の応力分布とすることとしています。つまり、骨組全体で「風上と風下の合計で長期荷重によるモーメントの影響を相殺して考えている」ということです。結果的には同様の計算をしていることになりますが、節点の耐力を求める前提をどう考えるかという点が異なります。例えばM16,M17 においても、長期荷重の影響についても図5の応力分布を仮定しています。節点において同じ条件で部材・接合部の耐力を比較するためには、最初から図5の応力分布を想定すべきということになります。
No.付2-3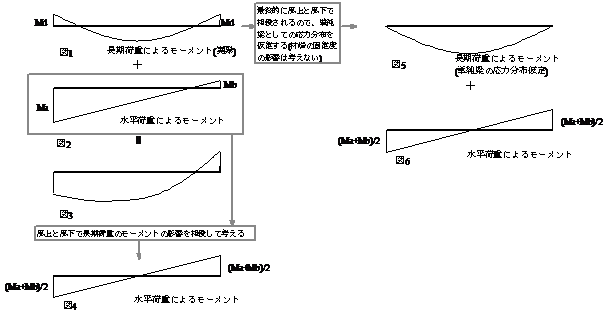
質問
表A2のMの考え方について
1.GMS(0.5L)及びGMS(0.25L)は、地震時鉛直荷重による単純梁応力と記載があります。この単純梁応力とは、平成8年版P51のピン-ローラ支点とした場合の応力でしょうか。長期応力が、梁母材の終局強度を超える場合があります。支点のモデル化を、調査建物に合わせて、ピン-ピンとして、長期応力を考慮してもよいと思います。
2.節点換算の耐力算定式M16,M17の導き方をお教え下さい。(出典等でも構いません)
回答
1.一端をピン支持、他端をピンローラ支持としたとき鉛直荷重による応力です。
なお、ここで示しているのはあくまでも標準的な架構を想定した場合の略算法です。調査建物に応じて適切に塑性解析を行っていただくことは問題有りません。
2.下図に示すように、風下側の接合部耐力と、はり中央位置(M17の場合ははり中間4分点)における部材耐力から分布荷重による単純ばり曲げモーメントを引いた耐力(分布荷重に対する抵抗分を引いた残りの曲げ耐力)で梁のメカニズムが決まる場合の、風上側の接合部に作用するモーメントです。
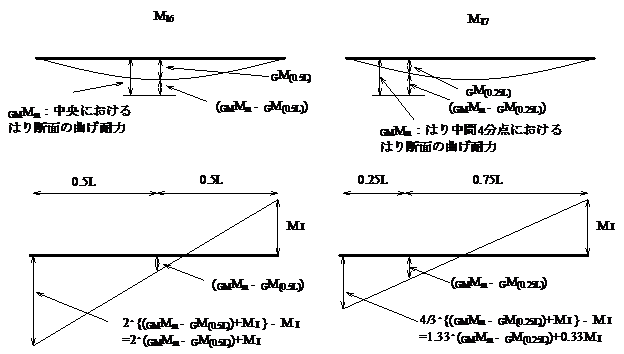
お問合せ先
大臣官房文教施設企画・防災部参事官(施設防災担当)付
-- 登録:平成22年10月 --