- 現在位置
- トップ > 教育 > 小学校、中学校、高等学校 > 全国的な学力調査について > 調査結果について > 平成19年度全国学力・学習状況調査追加分析結果 > .「全国学力・学習状況調査結果チャート」を用いた学力・学習状況に関する分析・検証手法の開発 > 「全国学力・学習状況調査結果チャート」の作成方法
「全国学力・学習状況調査結果チャート」の作成方法
別添
「全国学力・学習状況調査結果チャート」の作成の流れは、以下のとおりである。
- 表1及び表2に例示したように、教科学力の領域には、学力調査の各教科スコアを位置づけ、その他の領域は、児童生徒質問紙調査(又は学校質問紙調査)の中から該当する質問項目を選択し、設定する。
- これにより選出した質問紙調査の領域毎の対応項目の平均値を「全国学力・学習状況調査結果チャート」の各領域のスコアとして算出する。
- 全国、都道府県、市町村等を母集団として標準化する。
- 算出した領域ごとのスコアから、域内の学校の「全国学力・学習状況調査結果チャート」を作成する。
これを踏まえ、1~3における計算手順について以下に述べることとする。
なお、以下、用語の定義について示す
- 基礎値
個別の質問項目又は教科の結果から算出される値。「全国学力・学習状況調査結果チャート」作成の基礎となる数値 - 複合パラメータ
複数の質問項目の基礎値を平均したもの - スコア
「全国学力・学習状況調査結果チャート」における分析対象の各領域における値(基礎値や複合パラメータなどから算出)
1)分析対象と比較基準の決定
まず、「全国学力・学習状況調査結果チャート」を作成する単位である「分析対象」と、チャートにおいて「比較基準となる母集団」を決める。これに基づいて、「全国学力・学習状況調査結果チャート」の各領域のスコア(数値)を算出することとなる。
分析対象と比較基準となる母集団の組み合わせとしては、学校を分析対象とした場合、
- 全国を比較基準とする場合
- 各都道府県を比較基準とする場合
- 各市町村を比較基準とする場合
が考えられる。
2)分析対象の各領域のスコアの数と、それぞれの領域を構成する質問項目の決定
分析に用いる各領域のスコアの数と、個々の領域を構成する質問項目や教科学力のスコアを決定する。例えば、教科に関する調査の結果に関する各領域のスコアであれば、国語A及びB、算数/数学A及びBごとの平均正答率や、教科区分ごとの記述式問題の平均正答率などが考えられる。
また、質問紙調査の結果に関する結果であれば、例えば、児童生徒質問紙における「国語が好き」や「国語が大切と思う」などの質問項目で構成することが考えられる。
本書では、表1、表2に示す12の領域のスコアで「全国学力・学習状況調査結果チャート」の具体例を作成し掲載している。
3)質問項目に関する各領域のスコアの算出手順
手順1 各分析対象における基礎値の算出方法
(1-1)個別の質問項目ごとの値を算出する。
 教科に関する調査の結果を用いた基礎値の特定
教科に関する調査の結果を用いた基礎値の特定
教科区分別(国語A、国語B、算数/数学A、算数/数学B)の結果については、個別の分析対象ごとの平均正答率が基礎値となる。また、記述式問題や学習指導要領の領域ごとなど範囲を限定した調査問題の正答率を領域のスコアとする場合は、個別の分析対象ごとの記述式問題等の平均正答率が、当該領域における基礎値となる。
 児童生徒質問紙の質問項目に係る基礎値の算出
児童生徒質問紙の質問項目に係る基礎値の算出

(A1及びA2が肯定的な回答、A3及びA4が否定的な回答)
基礎値を、分析対象の質問紙調査の結果の割合(A1、A2、A3、A4)から近似的に計算する。
例えば、児童生徒質問紙調査の「国語の勉強はよく分かりますか」という質問で、学校の調査結果が、「当てはまる」27.0パーセント、「どちらかといえば当てはまる」35.0パーセント、「どちらかといえば当てはまらない」30.0パーセント、「当てはまらない」8.0パーセントの場合、その学校の当該質問項目の基礎値は、
4![]() 0.27
0.27![]() 3
3![]() 0.35
0.35![]() 2
2![]() 0.3
0.3![]() 1
1![]() 0.08
0.08![]() 2.81
2.81
となる。
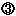 学校質問紙の質問項目に係る基礎値の算出
学校質問紙の質問項目に係る基礎値の算出
学校質問紙調査の質問項目においては、選択肢が4択のものと2択のものがあるため、すべて2択に置き直して、基礎値を算出する。
a)学校質問紙の質問項目に係る基礎値
・2択の質問項目の場合
- (肯定的な回答(はい)の場合)
- (否定的な回答(いいえ)の場合)
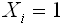
学校質問紙調査の質問項目が2択で肯定的な回答をしている場合は基礎値が「2」、否定的な回答をした場合は基礎値が「1」になる。
例えば、「学校の教育活動の情報について、ホームページを開設して情報提供を行っていますか」という質問で「はい」と答えている学校の当該質問項目の基礎値は「2」となる。
・4択の質問項目の場合
- (肯定的な回答のいずれかの場合)
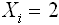
- (否定的な回答のいずれかの場合)
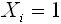
学校質問紙調査の質問項目が4択で肯定的な回答のいずれか選択している場合は基礎値が「2」、否定的な回答のいずれかを選択した場合は基礎値が「1」になる。
例えば、「第6学年の児童に対する国語の指導として、家庭学習の課題(宿題)を与えましたか」という質問で「よく行った」又は「どちらかといえば行った」と答えている学校の当該質問項目の基礎値は「2」となる。一方で、「あまり行っていない」又は「全く行っていない」と回答している学校の当該質問項目の基礎値は「1」となる。
b)教育委員会等における質問項目に係る基礎値
・2択の質問項目の場合

(A1が肯定的な回答、A2が否定的な回答)
基礎値を、分析対象の質問紙調査の結果の割合(A1、A2)から近似的に計算する。
例えば、学校質問紙調査の「学校の教育活動の情報について、ホームページを開設して情報提供を行っていますか」という質問で、ある市において「はい」と答えている学校の割合が70.0パーセント、「いいえ」と答えている学校の割合が30.0パーセントの場合、その市の当該質問項目の基礎値は、
2![]() 0.70
0.70![]() 1
1![]() 0.30
0.30![]() 1.7
1.7
となる。
・4択の質問項目の場合

(A1及びA2が肯定的な回答、A3及びA4が否定的な回答)
基礎値を、分析対象の質問紙調査の結果の割合(A1、A2、A3、A4)から近似的に計算する。
例えば、「第6学年の児童に対する国語の指導として、家庭学習の課題(宿題)を与えましたか」という質問で、ある市における学校の回答結果が、「よく行った」27.0パーセント、「どちらかといえば行った」35.0パーセント、「あまり行っていない」30.0パーセント、「全く行っていない」8.0パーセントとなっている場合、その市の当該質問項目の基礎値は、
2![]()
![]() 0.27
0.27![]() 0.35
0.35![]()
![]() 1
1![]()
![]() 0.30
0.30![]() 0.08
0.08![]()
![]() 1.62
1.62
となる。
(1-2)まとめる質問項目の値から、複合パラメータを算出する。
比較基準(全国、都道府県、市町村等)の複合パラメータと、分析対象の学校等についての複合パラメータを算出する。
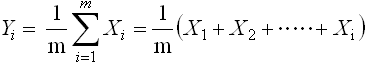
m![]() 複合させる基礎値の数
複合させる基礎値の数
(1-1)で計算した質問項目の基礎値を、領域ごとに足して平均を出すことで、複数の質問項目の複合パラメータの値を算出できる。
なお、文部科学省の公表資料から全国及び各都道府県の複合パラメータの算出を行うことができる。
手順2 標準偏差を算出する。
各学校等は、教科に関する調査の標準偏差については、文部科学省から提供されている資料から知ることができるが、質問項目を複合したパラメータに関する標準偏差を知るためには、比較基準となる主体に算出してもらう必要がある。具体的には、全国のものであれば文部科学省、都道府県全体であれば当該都道府県教育委員会、市町村全体であれば当該市町村教育委員会で算出することになる。
質問項目に関する複合パラメータの標準偏差を算出するための具体的な手順を、以下の(2-1)、(2-2)に示す。
(2-1)比較基準となる地域のすべての分析対象の複合パラメータの算出
(1-1)及び(1-2)の要領で、比較基準となる地域の域内すべての分析対象の複合パラメータを算出する。
(2-2)(2-1)で計算した複合パラメータから標準偏差を算出する。
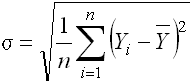
n![]() 比較基準(全国、都道府県、市町村等)の域内の分析対象(学校等)の数
比較基準(全国、都道府県、市町村等)の域内の分析対象(学校等)の数

参考に、全国を比較基準として、表1及び表2で示した「全国学力・学習状況調査結果チャート」を作成する際に必要となる平均値と標準偏差を表3及び表4に示す。
表3 「全国学力・学習状況調査結果チャート[児童生徒]」作成のための全国を比較基準とする複合パラメータの平均値および標準偏差一覧(平成19年度全国学力・学習状況調査)
| 領域番号 | 領域名 | 小学校調査 | 中学校調査 | ||||
|---|---|---|---|---|---|---|---|
| 平均値 | 標準偏差 | 平均値 | 標準偏差 | ||||
| 1 | 教科学力 | 国語A | 14.67 | 1.02 | 30.17 | 2.02 | |
| 2 | 算数/数学A | 15.58 | 1.35 | 25.74 | 3.29 | ||
| 3 | 国語B | 6.17 | 0.95 | 7.17 | 0.82 | ||
| 4 | 算数/数学B | 8.75 | 1.10 | 10.21 | 1.52 | ||
| 5 | 学習に対する関心・意欲・態度 | 国語への関心等 | 2.91 | 0.19 | 2.93 | 0.18 | |
| 6 | 算数/数学への関心等 | 3.20 | 0.20 | 2.90 | 0.18 | ||
| 7 | 総合的な学習への関心等 | 2.95 | 0.26 | 2.49 | 0.26 | ||
| 8 | 規範意識・自尊感情 | 規範意識 | 3.44 | 0.16 | 3.36 | 0.14 | |
| 9 | 自尊感情 | 3.23 | 0.19 | 3.02 | 0.16 | ||
| 10 | 学習の基盤となる体験・習慣 | 豊かな体験 | 3.08 | 0.20 | 2.93 | 0.19 | |
| 11 | 生活習慣 | 3.17 | 0.16 | 3.02 | 0.14 | ||
| 12 | 学習習慣 | 2.71 | 0.24 | 2.54 | 0.23 | ||
表4 「全国学力・学習状況調査結果チャート[学校運営]」作成のための全国を比較基準とする複合パラメータの平均値および標準偏差一覧(平成19年度全国学力・学習状況調査)
| 領域番号 | 領域名 | 小学校調査 | 中学校調査 | ||||
|---|---|---|---|---|---|---|---|
| 平均値 | 標準偏差 | 平均値 | 標準偏差 | ||||
| 1 | 教科学力 | 国語A | 14.67 | 1.02 | 30.17 | 2.02 | |
| 2 | 算数/数学A | 15.58 | 1.35 | 25.74 | 3.29 | ||
| 3 | 国語B | 6.17 | 0.95 | 7.17 | 0.82 | ||
| 4 | 算数/数学B | 8.75 | 1.10 | 10.21 | 1.52 | ||
| 5 | 教科指導 | 個に応じた指導 | 1.46 | 0.27 | 1.42 | 0.28 | |
| 6 | 国語科の指導法 | 1.77 | 0.20 | 1.77 | 0.21 | ||
| 7 | 算数/数学科の指導法 | 1.80 | 0.20 | 1.76 | 0.22 | ||
| 8 | 学力向上 | 児童生徒の状況 | 1.90 | 0.25 | 1.87 | 0.29 | |
| 9 | 学力向上に向けた取組 | 1.45 | 0.17 | 1.46 | 0.17 | ||
| 10 | 学校運営 | 地域の人材・施設の活用 | 1.56 | 0.23 | 1.58 | 0.19 | |
| 11 | 開かれた学校・学校評価 | 1.68 | 0.16 | 1.67 | 0.16 | ||
| 12 | 教員研修 | 1.85 | 0.17 | 1.75 | 0.21 | ||
手順3 データの標準化を行う。
手順1で求めた学校の複合パラメータの値と比較基準の複合パラメータの値、手順2で求めた標準偏差から、「全国学力・学習状況調査結果チャート」に用いる各領域のスコアZを以下のとおり、算出する。
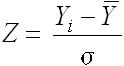
σ![]() 標準偏差
標準偏差
4)教科に関する各領域のスコアの算出
教科に関する調査結果の各領域のスコアについては、国語A、B、算数/数学A、Bのそれぞれの平均正答率と、比較基準となる平均正答率がそのまま各領域のスコアになる。
例えば、ある学校の算数Aの平均正答率が75.0パーセントで、基準とする都道府県内の学校の算数Aの平均正答率が70.0パーセント、標準偏差が4.2の場合、
![]() 0.75
0.75![]() 0.70
0.70![]()
![]() 4.2
4.2![]() 1.2
1.2
となり、都道府県を基準とした場合の当該学校の算数Aのスコア値は「1.2」と算出できる。
5)算出した各領域のスコアを組み合わせて「全国学力・学習状況調査結果チャート」を作成する
2)で算出した質問項目に関する領域のスコアと、3)で算出した教科に関する領域のスコアを用いて、「全国学力・学習状況調査結果チャート」を作成する。具体的には、「全国学力・学習状況調査結果チャート」の中心から、平均値との距離を一定とした円を引き、算出したそれぞれの項目の各領域のスコアを挿入して、「全国学力・学習状況調査結果チャート」が完成する。
-- 登録:平成21年以前 --