| 1. |
主題設定の理由 |
| |
「数学を学ぶ意義とはなんだろうか。」学ぶ立場の時は感じなかった疑問である。しかし数学を教える立場になり、最近「何のために数学を教えるのか」「この授業で何を伝えたいのか、何を伝えるべきなのか」と思うようになった。受験のために苦手とする数学を勉強する生徒や、今から高校数学を学ぼうとする生徒を目の前にしたとき、数学を学ぶ意義を説明する必要があるのではないかと感じる。確かに数学を学ぶことによって物事を数理的、論理的に処理する能力を身につけることも目的のひとつだが、数学の実用性を伝えることも大事だと考える。数学を実用する体験を通して、学習の動機付けもでき、数学に興味・関心を示してくれるのではないだろうか。三角比を利用して生徒の生活の場を測量することによって、数学の実用性を伝えたい。 |
| |
|
| 2. |
三角比の導入として伊能図を教材にする |
| |
三角比を学習したから測量するという段取りではおもしろみがない。数学という学問も必要に迫られた状況で人々が作り上げてきたもので、歴史を動かした文化である。測量をする必然性はどこにあったのか、歴史をたどって三角比を導入しようとも考えた。がしかし生徒を十分に納得させるだけの説明はなかなか難しい。そこで、ひとつの事柄に焦点を当て、深く掘り下げることにした。それが伊能忠敬という人物であり伊能図である。
また今年は経10研修でMs-PowerPointによる教材作成をする機会を得、文字のみでなく視覚・聴覚に訴えることができるというPowerPointの利点を生かして、伊能図を紹介することにした。 |
| |
|
| 3. |
授業の展開 |
| |
| (1) |
|
対象生徒 |
|
1年 |
|
5・6組 |
合同パート |
|
35名(男19名、女16名) |
| |
|
|
|
1年 |
|
7組 |
|
|
23名(男 9名、女14名) |
|
| |
| (2) |
|
実施日 平成12年10月10日(火曜日)から11月4日(土曜日)までの21時間 |
| (3) |
|
授業展開の計画(事業時数は実際の数) |
| |
|
| 三角比の導入(1時間) |
| |
PowerPointにより伊能忠敬の人物像と伊能図を紹介する(資料1)
学習後、測量するものを提示する。三角比の定義をする。 |
|
教科書(啓林館 高等学校 最新数学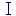 )を用いた学習(15時間) )を用いた学習(15時間) |
| |
1 鋭角の三角比 2 鈍角の三角比 3 正弦定理と余弦定理 4 図形の計量
章末問題 節ごとの小テスト 問題集エキスパート(数研出版)の演習
節ごとに小テストを実施して、基礎力を固める。教科書と平行して問題集の問題を取り上げて、実践力を養う。測量の資料綴じと角度を測る道具を作る作業を通して、実験への心構えを持たせる。 |
|
| 実測の計画・班(3〜4人)ごとの話し合い(1時間) |
| |
略図を描いて、式を立てる。実測するものを決める。求めたい値が出せるか、式を変形して確認する。
測量対象物の背景を説明して、学校環境への関心を持たせる。算出方法を教科書内容と照らし合わせて、既習事項を確認する。 |
|
| 実測と数値算出(1時間) |
| |
割り当てられた順序に従って実測する。実測が終了後、班ごとにレポートを作成して、一部ずつ提出する。 |
|
| 実測結果報告と検証(1時間) |
| |
各班の結果を発表して、算出方法を含めて比較検討する。スロープの傾斜角度の制限範囲に適合しているか調べる。アンケートをとる。 |
|
| 三角比の総まとめ(2時間) |
| |
基本問題と測量実験が生かせる問題を取り上げる。問題集の演習。 |
|
|
| |
|
|
| |
|
(資料1:PowerPointによる映像の内容・タイトル) |
| |
|
| 1 |
次の人を知っていますか? |
| 2 |
伊能忠敬像 |
| 3 |
伊能図 富士山周辺 |
| 4 |
伊能図 甲府盆地 |
| 5 |
伊能図 竜王町〜甲府市 |
| 6 |
伊能図 石和〜勝沼 |
| 7 |
伊能図 舞鶴城 |
| 8 |
伊能図 身延山久遠寺 |
| 9 |
伊能図 富士山沼津 |
| 10 |
伊能忠敬の略歴 |
| 11 |
大日本沿海與地全図 |
| 12 |
17年間の旅のきっかけと彼の目的 |
| 13 |
精密な地図 何で測ったのか |
| 14 |
測量道具 杖先方位盤 |
| 15 |
測量道具 象限儀 |
| 16 |
測量道具 量程車 |
| 17 |
測量道具 半円方位盤 |
| 18 |
測量の図 |
| 19 |
さあ みんなも測ってみよう |
| 20〜28 |
測量課題問題(資料2) |
| 29 |
正確なデーターを出すために |
|
| |
|
|
| |
|
| 転載元 |
|
2、15、16、17、18 はがき(伊能忠敬記念館) |
| |
|
3〜9 国立国会図書館電子展示会ディジタル貴重書展(インターネット) |
| |
|
11、14「歴史誕生 11」(角川書店) |
|
|
| |
|
| 4. |
実測課題問題と教科書問題の対応 |
|
三角比学習後に測量する実践は今までにもあったが、校庭の木の高さなど対象物は1つに限られていた。しかし三角比の応用解法は他にもあり、せっかく時間を費やして校庭に出るのであれば、教科書に載っている内容に匹敵する対象物を取り上げようと、校庭を見回し次の6つの対象物を見つけた。 |
| |
|
| |
| 測量課題問題(資料2) |
課題に対応する教科書内容 |
| 1.後者の高さ |
P110 例題1 |
| 2.ロータリーの木の高さ |
P132 章末問題A3 |
| 3.部室の階段の高さと長さ |
P112 例題2 |
| 4.スロープの傾斜角度 |
P109 問4 |
| 5.青空像が立っている芝生の円の半径 |
P122 問21 |
| 6.池向こうの松の高さ |
P130 問35 |
|
| |
|
| |
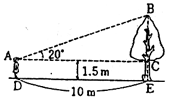
| P110 例題1 |
木の根もとEから10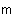 離れた地点Dで、木の先端Bを見上げる角を測ったら、20 離れた地点Dで、木の先端Bを見上げる角を測ったら、20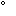 であった。 であった。
目の高さを1.5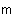 として、この木の高さBEを求めよ。 として、この木の高さBEを求めよ。 |
|
 |
|
| |
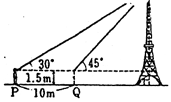
| P132 章末問題A3 |
右の図のように、ある地点Pから塔の先端を見上げる角が30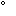 であった。 であった。
Pから塔の方向へ10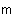 進み、その地点Qから塔の先端を見上げる過度を測ったら、45 進み、その地点Qから塔の先端を見上げる過度を測ったら、45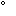 であった。 であった。
目の高さを1.5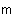 として、塔の高さを求めよ。 として、塔の高さを求めよ。 |
|
 |
|
| |
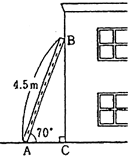
| P112 例題2 |
長さ4.5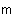 のはしごABを右の図のように壁に立てかけると、はしごと地面とのつくる角は70 のはしごABを右の図のように壁に立てかけると、はしごと地面とのつくる角は70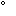 であった。 であった。
はしごの先端の高さBCは約何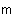 か。また、はしごの根もとから壁までの距離ACは約何 か。また、はしごの根もとから壁までの距離ACは約何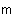 か。 か。 |
|
 |
|
| |
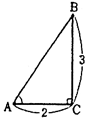
| P109 問4 |
| 次の直角三角形ABCで、角Aの大きさを求めよ。 |
| (1) |
 |
|
(2) |
 |
|
| |
| P122 問21 |
三角形ABCで、A 45 45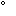 、B 、B 75 75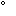 、C 、C 2 2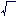 3のとき、三角形ABCの外接円の半径を求めよ。 3のとき、三角形ABCの外接円の半径を求めよ。 |
| |
| P130 問35 |
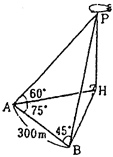
飛行船の高さを測るために、2地点A、Bから飛行船Pとその真下の点Hを観測して、AB 300 300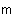 、角HAB 、角HAB 75 75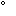 角HBA 角HBA 45 45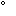 、角PAH 、角PAH 60 60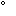 を得た。飛行船の高さPHを求めよ。 を得た。飛行船の高さPHを求めよ。
ただし、A、B、Hは同じ水平面上にある。 |
|
 |
|
|
| |
|
| 5. |
測量実験の結果(資料3)と考察 |
|
解答方法は4で示した教科書内容を予想していたが、生徒の発想は豊かでかつ柔軟で興味深かった。計画はさほどスムーズに進んだわけではなかったが、課題と教科書を比べながら班の話し合いがなされた。測量には生徒が作った角度を測る道具以外に、メジャー、ロープ、遊戯用の長いゴムひも、サッカー部使用のポール、三点の目印にする金具を用意した。結局測る順番を決めず自由に活動させたが、メジャーが全部の班にいき渡らなかった5・6組では2班で1つのものを利用するところもあり不便だった。
また偶然にもこの11月1日は計量の日であり、しかもNHK総合テレビ「その時歴史は動いた」で伊能忠敬を取り上げた日であった。 |
|
|
|
<考察> |
| |
| 1. |
校舎の高さ(15.9メートル) |
|
教科書例題1と同様の解答。仰角を45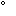 に設定したところと、その場で仰角を決めた班に分かれる。 に設定したところと、その場で仰角を決めた班に分かれる。 |
|
| 2. |
ロータリーの木の高さ |
|
教科書問題B2と同様に、仰角30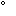 と45 と45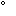 の2地点の距離から求めるものがほとんどである。庭園の中に入れないことを無視して計画を立ててしまった班もある。その中でも庭園を横に見ながら距離を測って結果を出したところもある。 の2地点の距離から求めるものがほとんどである。庭園の中に入れないことを無視して計画を立ててしまった班もある。その中でも庭園を横に見ながら距離を測って結果を出したところもある。 |
|
| 3. |
部室の階段の高さ(約2.8メートル)と長さ(約4.8メートル) |
|
正弦定理を用いるもの、正弦と三平方の定理の組み合わせ、正接と余弦、正接と正弦で求めるものがある。階段の傾斜角度は一定(35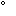 )のはずであるが、数値のばらつきがあり角度の測り方が理解できていなかったことに気づく。 )のはずであるが、数値のばらつきがあり角度の測り方が理解できていなかったことに気づく。 |
|
| 4. |
スロープの傾斜角度 |
|
2辺の長さから、正接、正弦、余弦のいずれかを計算して求めるのが一番簡単な方法だと思うが、余弦定理を用いたことは予想外だった。余弦の値が1よりも大きいものがあり、余弦のとる値の範囲を確認することとなった。また、傾斜角度の基準「12分の1以下」を満たしている(校舎の設計図も同様に書かれている)ことから4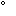 以下が妥当であると思われる。 以下が妥当であると思われる。 |
|
| 5. |
青空像が立っている芝生の円の半径(2.5メートル) |
|
円周から割り出しているもの、内接三角形を作り正弦定理を用いるもの、逆に外接する三角形を作り内接円の半径として求めるもの、直角三角形を想定して三平方の定理を用いるものがある。円周から割り出しているものが他の方法に比べ正確な値が出たが、他のものは厚みのあるロープを使ったのでロープの内側・外側では誤差が生じやすいのではないか。 |
|
| 6. |
池向こうの松の高さ |
|
池の幅や空間上の実測不可能な角度などがあり、計画どおりには進まなかったところがほとんどだったが、課題に取り組んだ意義はあった。 |
|
|
| |
|
| 6. |
アンケート結果と生徒の感想 |
|
| (1) |
PowerPointによる映像に何とタイトル名をつけますか。 |
|
「伊能忠敬・人生と測量」「伊能忠敬と日本地図」「日本初の日本地図」「伊能忠敬の旅」「日本地図の歴史」「日本地図の父−伊能忠敬−」「世界の伊能忠敬」「世界の描き方」「伊能忠敬の測量日記」「テーマ:明日をゆく人々」「日本を眺めた男」「日本地図の原点」「伊能忠敬−日本を測った男−」「伊能忠敬の足あと」「伊能忠敬の測量法を盗み活用せよ」「特別番組 日本測量の父 伊能忠敬の波乱の人生−日本の測量はこうして進化した−」 |
| |
|
| (2) |
伊能忠敬に関する感想 |
|
| ・ |
現在のような最新の測量器具もなかった江戸時代に、自分の足と昔の器具を使って日本地図を正確に書いた伊能忠敬にびっくりした。 |
| ・ |
今の地図とあまり変わりがないことに驚いた。たった数個のアイテムだけであんなに正確な地図が作れるとはすごい。しかも自分達も測量すると聞いて、その時は「無理だろ」なんて思っていた。 |
| ・ |
伊能忠敬さんが地理や日本史でしか出てこないと思っていたが、意外なところで出てきておもしろかった。地図を歩いて作成したことは知っていたけれど、詳しい方法は全く知らなかったので、いい勉強になった。 |
| ・ |
伊能忠敬さんが生きているうちに地図が完成すれば良かった。 |
| ・ |
江戸時代にはもうすでに正確な測量技術があったことに驚いた。 |
| ・ |
測量器具に実際に触れられたらおもしろいかもしれない。 |
| ・ |
社会で勉強したり、テレビで何度か特集を見たことがあるので大体知っていたが、もしこの人が地図を作らなかったら今の地図はあったのかな。 |
| ・ |
地理と数学の結びつきを感じた。 |
| ・ |
当時は日本の形など想像がつかなかったと思うが、計量によって上から見たように地図を作り上げてしまった伊能忠敬は、すばらしい知識と執念を持っていたのだと思う。伊能忠敬は現在の日本人よりも、この日本を知っていたのかもしれない。 |
|
| |
|
| (3) |
測量実験に関する感想 |
|
| ・ |
30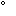 や45 や45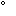 と角度を決めてから測る場合、その角度になる位置を探すことに時間がかかった。 と角度を決めてから測る場合、その角度になる位置を探すことに時間がかかった。 |
| ・ |
実測した値と実際の値に誤差があって残念だったが、これだけの材料と三角比の色々な公式で長さが求めることができるということに驚いた。 |
| ・ |
測量するのがこんなに大変とは思わなかった。一番大変だったのは小数の計算だった。 |
| ・ |
自分達で初めから計画を立て、その計算式で実際に長さや角度を求めることは、とても楽しいし役に立つと思う。 |
| ・ |
計画自体がしっかりできてなかったから、測量できないものがあった。計画は多くのことを考慮してすることが大切だとわかった。 |
| ・ |
角度の測り方を理解していなかった。メジャーの測り方もできていなかったように思う。 |
| ・ |
「ここは測れる」と思っていたところが、やってみたら測れなかった。もう少し別の方面から考える、頭の柔らかさが必要だった。 |
| ・ |
実際に測るのと紙の上でシミュレーションするのでは、やはり違うと思った。 |
| ・ |
班みんなで協力できて良かった。 |
| ・ |
の班の計算式などを見て、いろいろなやり方があって関心した。 |
| ・ |
少しの角度の違いでも長さなど結構変わってしまうと気づいた。授業では30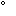 45 45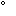 60 60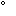 ・・・・150 ・・・・150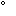 など限られた角度で三角比を求めたが、実際はもっと細かい計算をしていた。 など限られた角度で三角比を求めたが、実際はもっと細かい計算をしていた。 |
| ・ |
しっかりとした実測をしないと、全然違う値になってしまう。 |
| ・ |
ちょっと甘く考えていた所がある。「だいたい」とか「このくらいかな」という値が後々ひびいて、値を少しずつ変えてしまったのだと思う。“正確性”が大切ですよね。 |
| ・ |
建物や木の高さを測るのに、別の場所の長さや角度を測らなくてはいけないことがわかった。測量はいろいろな難しい計算を使ったり、すごく大変だと思った。 |
| ・ |
いろいろな所が測れて楽しかった。 |
| ・ |
分度器の道具の上にストローか何かをつけて、もっと正確に角度を測ったら良かった。 |
| ・ |
班によって実験結果が大きく異なったりして答えが一致しなかったが、自分達で取り組んでレポートを作ることはとてもおもしろかった。 |
|
| |
|
| (4) |
三角比の授業を通しての感想 |
|
| ・ |
測量に使えて実用的な三角比の勉強ができたと思う。 |
| ・ |
紙の上で実際の長さ、大きさがわかることはすごいと思った。知らないとできないことなので、ちょっと得した気分。 |
| ・ |
三角比を使って測ることによって、三角比の使いまわしができるようになった。ものを測ることの難しさがよくわかった。 |
| ・ |
授業でやったことの実用性を知ることもできて良かった。 |
| ・ |
教科書の中でやってても「だからなによ」という気になるけど、実際にある実測不可能という感じのものを工夫を凝らして謎解きの如く値を出すのは、なかなか楽しいし納得する。直接測っていないのに、答えが近いときはうれしい。 |
| ・ |
図形はあまり必要ないとか苦手とか思っていたが、この三角比は測量など建築や社会の色々なことに役立っていることがわかった。 |
| ・ |
計画を立てている時に、自分が仕事をしているような錯覚をすごく感じた。課題を通して今までの勉強と違って身近に感じた。 |
| ・ |
すごく楽しかった。今までは知ることのできなかった角度や長さをこれからは知ることができて、本当にいい勉強になった。 |
| ・ |
測量はもっと難しいことをするのかと思っていたが、基本的な公式や定理で答えが出たので驚いた。 |
| ・ |
いろいろなものの長さが測れるようになった。日常生活で測りたいものがあったら、三角比を活用した。 |
| ・ |
最初はよく理解していたけれど、だんだん難しくなってきて大変だった。でも、測量していろいろなことが一気に復習できた。 |
|
| |
|
| (5) |
数学という教科に対する感想 |
|
| ・ |
やっぱり数学は難しい。 |
| ・ |
以前はお金が数えられれば人生平気さと思っていたけれど、ものを作ったりするのに数学はやっぱり必要なものなんだな。 |
| ・ |
数学がおもしろくなった。机の上だけでやるものではないんだと思った。いろんな事に利用できるし、解けたらうれしくなる。 |
| ・ |
公式をつくり出した人やどんな過程で公式が生まれたのか、知りたくなった。ただの受験のための科目ではなく、自分で答えを出す知識や発想力が身についていく科目だと思う。 |
| ・ |
応用が利くし、考え方を勉強できて楽しい。 |
| ・ |
意外とおもしろく、やりがいがあると思う。 |
| ・ |
世の中にはたくさんの公式や法則があり、それをうまく活用すれば未知の値が得られることがいいところだと思った。 |
| ・ |
数週間前は数学は役に立たないと思っていたが、数学の力を使って物の高さなどを測れることを知って、数学の大切さがわかった。 |
|
|
| |
|
| 7. |
まとめ |
|
| (1) |
実践の成果について |
|
数学の実用性を伝えることは概ねできた。計算は多少複雑で数学への印象が変わらなかった生徒もいたようであるが、実験することで計画から測量、レポートつくりまで自分達の手で作り上げた達成感と、既習事項の定着が計れたと思う。学習した内容がどんな場面で生きてくるのか、受験のための数学ではなくて本来は生活するための学問であることを感じ取ってくれたと思う。
この研究を通して、問題を解決するプロセスを自分で考え有効かどうかを判断することは、解決した時に感じる喜びに必要不可欠のものであると痛感する。また問題解決できてこそ、学習した意義が自ずと理解できるのではないだろうか。
折しも、この実践前の地理の授業で伊能図を学習し、また美術では水彩で校庭を描く授業が展開されており、教科の枠を越えた学習にもなっていたようである。生徒に「三角比の分野だけが社会に役立っている」と思われないように、他の分野についても研究を深めていきたい。 |
| |
|
| (2) |
情報機器の活用について |
|
今回の研究を通して、新しいことがいろいろあった。Ms-PowerPointによるプレゼンテーションを作ること、デジタルカメラの画像や書物の情報をスキャナーを用いてパソコンに取り入れることなど。情報処理に詳しい先生方にお手伝いいただいたわけであるが、今更ながら情報機器の幅広い応用力に驚いてしまった。生徒が昼休みや放課後に図書館や情報処理室でパソコンで遊んだり、パソコンから情報を得て進路指導やホームルーム指導をする時代である。益々、情報機器を使いこなす必要性を感じる。 |
|