| 学習のねらいと発問 |
学習活動 |
評価・配慮事項 |
1 課題の把握
数の大小,文字式の大小を比較する |
問題1
| |
2と3はどちらが大きいか? |
| |
2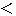 3である 3である |
問題2
多くの生徒が 2a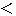 3a と答える 3a と答える |
|
2a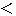 3a となるのはなぜか。 3a となるのはなぜか。 |
| ◎ |
2より3の方が大きいから。 |
| ◎ |
aが2つより,aが3つの方が大きいから。 |
| ◎ |
すべての場合にこのようになる。 |
| ◎ |
2a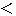 a にならないときもある。 a にならないときもある。
|
| ◎ |
a 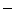 2だと,2a 2だと,2a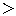 3a となる。 3a となる。 |
|
生徒の多くは,正の数を考えているものと思われる。その考えをどのようにして,0や負の数に拡げるかについて配慮して指導する。 |
2 解決の見通し
2a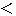 3a にならないときとはどのようなときか。 3a にならないときとはどのようなときか。 |
aがどのような数であるかが分からないので,2a ,3a のままでは,大小を比較することができない。aはどんな数であるかを考えることが必要である。 |
【数学への関心・意欲・態度】
今まで,当たり前と思っていたこと以外の結果があることに関心を示したか。
中学校で新たに学習した数について想起させる。
その数も,正の数の場合と同じ結果になるかについて,確認する。 |
3 問題の解決
aをどのような数と考えることが必要か。
大小を比較するとは,何を比較することか。
文字aに具体的な数値を代入することにより2aと3aの大小が判別できる。 |
a 2の場合 2の場合
2a 2 2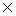 a a 2 2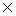 2 2 4 4
3a 3 3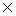 a a 3 3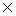 2 2 6 6
a 2の場合は, 4 2の場合は, 4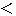 6となるので,2a 6となるので,2a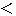 3a である。 3a である。
a 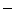 2の場合 2の場合
2a 2 2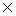 a a 2 2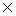 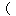 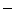 2 2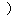  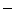 4 4
3a 3 3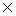 a a 3 3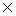 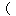 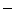 2 2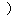  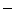 6 6
a 2の場合は, 2の場合は,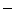 4 4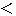 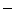 6となるので,2a 6となるので,2a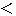 3a である。 3a である。
a 0の場合 0の場合
2a 2 2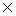 a a 2 2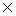 0 0 0 0
3a 3 3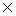 a a 3 3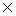 0 0 0 0
a 0の場合は, 0 0の場合は, 0 0となるので,2a 0となるので,2a 3a である。 3a である。
|
【数学的な見方や考え方】
どのような場合分けが必要であるかを考えることができるか。
大小を考えるとき,数を場合分けをすることが必要であることを指導する。
正の数,負の数の場合1つの例しか計算していないが,それ以外でもいえるのかについて,生徒に考えさせる。
|
4 解決方法の検討
これまでに計算したことが数学的にどのような意味を持つか考える。 |
| ◎ |
数は正の数,0,負の数の場合がある。それぞれの場合によって結果が違ってくる。 |
| ◎ |
文字はいろいろな数になることがある。これらの場合について,考えることが必要である。 |
| ◎ |
文字をある数に置き換えて,計算した結果を比較することが必要である。 |
| ◎ |
文字をある数に置き換えることを代入するという。また,代入して計算した結果を式の値という。を考えることが必要である。 |
|
今まで,行った活動は,数学的にはどのような意味があるかを確認する。 |
5 まとめ
代入,式の値という用語を使って,2aと3a がどちらが大きいかを比較するときの方法を説明する。 |
文字式の文字にある数を代入して,式の値を求め,その式の値によって,大小を比較する。
代入する数は,正の数,0,負の数の場合を考えることが必要である。 |
数学の用語を学習した後に,その用語を使って学習したことを説明する。 |