| (1) |
平成13年度小中学校教育課程実施状況調査結果の概要 |
| |
|
| |
【小学校】 |
| |
| <調査結果の特色> |
| ○ |
いずれの学年でも、設定通過率との比較では、上回る又は同程度と考えられるものが半数以上。同一問題での比較では前回を有意に下回るものが過半数。 |
| ○ |
計算の意味理解、三角形や円の面積の問題などで設定通過率を下回る状況。 |
| ○ |
「思考・判断」についての問題で設定通過率を下回ると考えられるものが多い状況「いろいろな考え方を発表し合うのは楽しい」、「問題が解けたとき、別な解き方を考えようとする」という質問に対し、肯定的な回答をする児童の得点が高い傾向。 |
|
|
| <指導上の改善点> |
| ○ |
計算の意味を実際の場面と結び付けたり、面積の公式を児童自らが工夫してつくっていく学習などを充実させるとともに、計算の技能を定着させるための指導を一人一人の学習状況に応じて進めるための指導法の改善が必要。 |
| ○ |
数量や図形についての作業的・体験的な活動等を取り入れることなど、指導法の改善を図るとともに、児童が様々な考え方を試みたり話し合ったりする中で、日常生活で数を用いることの有用性など数理的な処理のよさを実感できるようにすることが必要。 |
|
|
|
| |
|
| (2) |
学習指導の改善
平成13年度小中学校教育課程実施状況調査教科別報告書(小学校 算数)抜粋 |
| |
|
| |
| 8 |
「図形の面積の求め方」 |
|
「図形の面積の求め方」の結果の概要
「図形の面積の求め方」にかかわる問題は小問で10問である。今回の結果は,設定通過率と同程度と考えられるものが2問,下回ると考えられるものが8問であった。前回調査との同一問題が3問あり,今回の結果は,前回と有意に差のないものが1問,前回を有意に下回るものが2問であった。
以下では,5年B7の問題を取り上げて結果について考察する。 |
|
| |
|
| |
| ア |
問題 |
| |
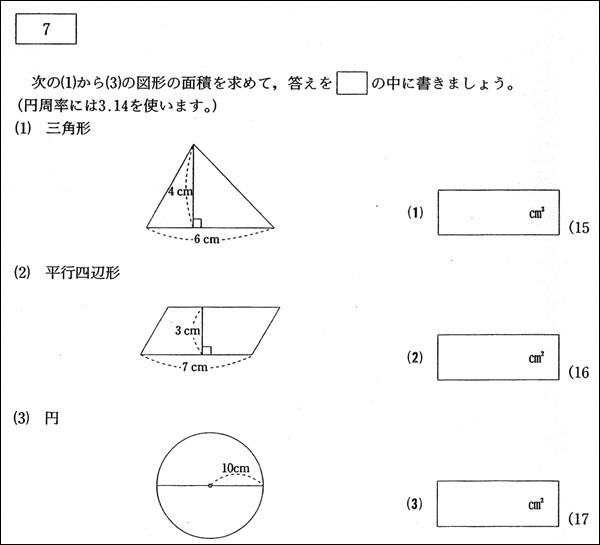 |
| |
|
| イ |
出題のねらい |
| |
本問題は,学習指導要領の「5年・量と測定(1)」の内容についての出題である。出題のねらいは,「三角形,平行四辺形,円の面積を求める」ことの学習の実現状況をみるものである。評価の観点は,「数量や図形についての知識・理解」である。 |
| |
|
| ウ |
今回の結果 |
| |
小問ごとの通過率 |
| |
  内は公立学校での通過率 内は公立学校での通過率 |
| 問題番号 |
評価観点 |
過去問 |
記述式 |
今回通過率 |
設定通過率 |
前回通過率 |
有意差の有無 |
| B7(1) |
知識・理解 |
 |
|
73.8
 73.5 73.5 |
85 |
84.8 |
 |
| B7(2) |
知識・理解 |
 |
|
89.9
 89.8 89.8 |
90 |
90.4 |
|
| B7(3) |
知識・理解 |
 |
|
53.7
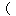 53.3 53.3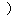 |
75 |
69.1 |
 |
|
|
| |
|
| |
解答類型ごとの反応率 |
| |
| 問題番号 |
解答類型 |
反応率 |
|
(1) |
12 と解答しているもの |
 1 1 |
73.8 |
| 24 と解答しているもの |
2 |
18.0 |
| 上記以外の解答 |
9 |
5.2 |
| 無解答 |
0 |
3.1 |
| (2) |
21 と解答しているもの |
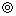 1 1 |
89.9 |
| 上記以外の解答 |
9 |
6.6 |
| 無解答 |
0 |
3.6 |
| (3) |
314 と解答しているもの |
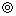 1 1 |
53.7 |
| 31.4 と解答しているもの |
2 |
6.7 |
| 62.8 と解答しているもの |
3 |
9.9 |
| 上記以外の解答 |
9 |
17.9 |
| 無解答 |
0 |
11.8 |
|
| |
|
| エ |
結果の考察 |
| |
(1)について
B7(1)は,三角形の面積の求め方についての理解を問うものである。設定通過率は85%である。今回の通過率は 73.8%であり,設定通過率を下回ると考えられる。
24という誤答の反応率が 18.0%ある。そうした誤答の中には,「三角形の面積 底辺 底辺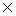 高さ 高さ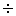 2」という公式を理解していないものや,公式を覚えているが,計算するときに2で割ることを忘れるなど正しく使えないものが含まれていると考えられる。なお,児童の実際の解答を調べてみたところ,(1)で「24」と誤答した児童のうちの多く(約8割)が,次の(2)の問題(平行四辺形の面積)では,正しく「21」と解答している。児童の解答をみると,式をかいているものと,式をかいていないものの両方がある。 2」という公式を理解していないものや,公式を覚えているが,計算するときに2で割ることを忘れるなど正しく使えないものが含まれていると考えられる。なお,児童の実際の解答を調べてみたところ,(1)で「24」と誤答した児童のうちの多く(約8割)が,次の(2)の問題(平行四辺形の面積)では,正しく「21」と解答している。児童の解答をみると,式をかいているものと,式をかいていないものの両方がある。
B7(1)は前回調査と同一問題であり,今回の結果は前回を有意に下回っている。
また,B7(1)の類題として,三角形の面積を求める式をかかせる問題(5年A7)がある。その解答の中でも,2で割ることを忘れている誤答(8.8%)がみられる。
(2)について
B7(2)は,平行四辺形の面積の求め方についての理解を問うものである。設定通過率は90%である。今回の通過率は89.9%であり,設定通過率と同程度と考えられる。児童の実際の解答をみると,上記以外の解答の例として,「10.5」という誤答や,「3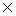 7 7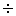 2」という誤った式をかいているものがある。 2」という誤った式をかいているものがある。
また,B7(2)は前回調査と同一問題であり,今回の結果は前回と有意に差はない。
(3)について
B7(3)は,円の面積の求め方についての理解を問うものである。設定通過率は75%である。今回の通過率は53.7%であり,設定通過率を下回ると考えられる。
児童の解答の中には, 31.4 という誤答をしているものがある。これは,半径である10を用いて10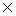 3.14 という計算をしているとみられる。また,62.8 という誤答もある。これは,直径である 20を用いて20 3.14 という計算をしているとみられる。また,62.8 という誤答もある。これは,直径である 20を用いて20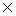 3.14 という計算をしているとみられる。こうした誤りの中には,円の面積の公式を理解していないものや,公式は覚えているが正しく使えないものが含まれていると考えられる。 3.14 という計算をしているとみられる。こうした誤りの中には,円の面積の公式を理解していないものや,公式は覚えているが正しく使えないものが含まれていると考えられる。
B7(3)は前回調査と同一問題であり,今回の結果は前回を有意に下回っている。 |
| |
|
| オ |
「図形の面積の求め方」の指導上の改善 |
|
図形の面積公式の理解を定着させるために,面積を求める際には,そこで用いる公式をかいたうえで計算するようにするとよい。式をかくことによって,学習の途中で誤った場合などに,どこにその原因があるかを確認することもできるようになるからである。
B7(1)の問題では,三角形の面積を求めるときに,2で割ることを忘れる誤りがみられた。そうした誤りが,公式をよく理解していないことによるものなのか,あるいは単にうっかりした誤りなのかを確かめるようにするなど,学習の過程を振り返ることができるようにする指導の工夫が大切である。
円の面積を求める公式の学習では,公式をただ暗記するだけでは確実な定着を図ることができない。そのため,例えば,方眼紙を用いて円に含まれる正方形の個数を数えてみたり,面積公式を自分たちでつくってみたりするなどの学習を積極的に取り入れるようにするとよい。
また,例えば,「半径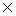 半径 半径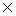 3.14」という公式が,半径の長さを一辺とするような正方形の面積の3.14倍を表しているととらえるなど,式の意味を読みとるような活動を取り入れるとよい。それによって,公式の意味理解を深めたり,円の面積の大きさを実感的にとらえたりすることができるようになるからである。 3.14」という公式が,半径の長さを一辺とするような正方形の面積の3.14倍を表しているととらえるなど,式の意味を読みとるような活動を取り入れるとよい。それによって,公式の意味理解を深めたり,円の面積の大きさを実感的にとらえたりすることができるようになるからである。
さらに,つくり出した公式を様々な場面で用いたり,問題解決の場で活用したりするなどして,繰り返し用いる学習場面を設定し,学習した内容の定着を図る指導が必要である。そのために,身の回りにある様々な図形の面積を調べたり,比べたりする学習を取り入れるとよい。また,面積の公式を活用する場面として,これまでに算数の授業で取り上げてきた様々な図形について,それらの面積の求め方を考える学習があげられる。そうした学習によって,基本的な図形の面積公式の理解が深まり,活用する力が高まるようになると考えられる。 |
|
| |
|
| |
上記の指摘を受け,授業展開された実践例 |
| |
|
| |
(実践例1)円の円周と直径の関係を調べる |
| |
| ねらい: |
子どもたち自身による作業的・体験的な活動を通して,円周率の意味や,その大きさを実感をともなって理解できるようにする |
|
| |
|
| |
| 学習のねらい |
学習活動 |
指導上の留意点
評価など |
| 円周と直径の関係を調べる |
「円のまわりの長さは,直径の長さのおよそ何倍になっているでしょうか。」 |
・黒板に図を貼って説明し,これから調べようとする事柄を明確にする。
|
作業的・体験的な活動を通して図形の意味や性質を理解する
|
「3人で手をつないで,きれいな円を作ってみよう。」
「作った円の中に,もう一人の子どもが入り,中心に立って,手をのばしてみる。」
「円のまわりの長さは,3人分の長さ。直径の長さは,1人分の長さになっている。」
「数人のグループに分かれて,実際に調べてみよう。」 |
・人が手を伸ばしたときの長さは,ほぼ身長に等しい。
・教室の中などに,子どもたちが自由に活動できるスペースを用意する。 |
| 3人以外の場合についても調べる |
「3人でないときは,どうなるのだろうか。」
「円を作るときの人数が,4人のとき,5人のとき,6人のときは,どうなるだろうか。」
「6人で円を作ると,直径の長さは,2人分の長さになっている。」 |
【数量や図形についての知識・理解】
円周の長さが,直径のおよそ3倍になっていることを,子ども自身の活動を通して調べて,豊かな感覚をともなって理解できるようにする。
|
| 色々な場合について調べ,そこに共通している性質を見つける |
「身のまわりにある色々な円の形について,円周と直径の長さを調べてみよう。」
次のものを実際に調べる
・音楽用のCD
・一輪車のタイヤ
・体育館の床にかいていある円 |
|
| |
|
| |
(実践例2)円の面積の大きさを調べる |
| |
| ねらい: |
円の面積の公式をもとにして,円の面積の大きさを調べ,その大きを実感をともなって理解できるようにする |
|
| |
|
| |
|