| (ア) |
高等学校における数学の基礎的な内容を一層明確にするとともに、多様化した生徒の実態により的確に対応できるようにするため、現行の科目を再編成し、「数学I」、「数学 」、「数学 」、「数学 」、「数学A」、「数学B」及び「数学C」の科目を設ける。 」、「数学A」、「数学B」及び「数学C」の科目を設ける。 |
| (イ) |
「数学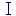 」、「数学 」、「数学 」及び「数学 」及び「数学 」は、その内容をすべて履修させることを原則とし、次のように内容を構成する。 」は、その内容をすべて履修させることを原則とし、次のように内容を構成する。
「数学I」は、中学校の数学の内容との関連を踏まえ、例えば、関数、図形、数列、確率など基礎的な内容で構成する。その際、日常の事象との関連にも配慮する。また、生徒の実態に応じ内容の弾力的な取扱いができるよう配慮する。
「数学 」は、「数学I」に続く科目で、例えば、関数、図形などのより広い範囲の基礎的な内容で構成する。 」は、「数学I」に続く科目で、例えば、関数、図形などのより広い範囲の基礎的な内容で構成する。
「数学 」は、「数学 」は、「数学 」に続く科目で、例えば、微分、積分を中心とした内容で構成する。 」に続く科目で、例えば、微分、積分を中心とした内容で構成する。 |
| (ウ) |
「数学A」、「数学B」及び「数学C」は、生徒の能力・適性、興味・関心、進路等にに応じて、その内容を部分的に選択して履修させることを原則とし、次のように内容を構成する。
「数学A」は、例えば、数と式、平面幾何などで構成する。
「数学B」は、例えば、数列と級数、複素数平面などで構成する。
「数学C」は、応用数理の観点に立ち、コンピュータを活用する内容を中心にして構成する。 |
| (エ) |
「数学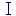 」は、低学年においてすべての生徒に履修させることとする。また、「数学A」は、「数学 」は、低学年においてすべての生徒に履修させることとする。また、「数学A」は、「数学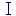 」と並行あるいは「数学 」と並行あるいは「数学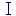 」に続いて履修させることとし、「数学B」及び「数学C」については、「数学I」を履修した後に履修させるようにする。 」に続いて履修させることとし、「数学B」及び「数学C」については、「数学I」を履修した後に履修させるようにする。 |
| (オ) |
幾何については、中学校の数学の内容との関連に配慮し、論理的な思考力や直観力を養う観点から、論証幾何や複素数平面を取り扱うことができるようにする。確率・統計については、確率の基礎的な内容はすべての生徒に履修させることとし、統計処理の内容はコンピュータと関連付けて取り扱うようにする。 |
| (カ) |
各科目の指導に当たってはコンピュータ等を活用することについて配慮する。 |