戻る
資料５−３

評価基準の作成，評価方法の工夫改善のための参考資料（高等学校）
−評価基準，評価方法等の研究開発（報告）−　（抜粋）

第４節　数学

第 １　教科目標，評価の観点及びその趣旨

１ 　教科目標
　数学における基本的な概念や原理・法則の理解を深め，事象を数学的に考察し処理する能力を高め，数学的活動を通して創造性の基礎を培うとともに，数学的な見方や考え方のよさを認識し，それらを積極的に活用する態度を育てる。
２ 　評価の観点及びその趣旨
関心・意欲・態度 数学的な見方や考え方 表現・処理 知識・理解
数学的活動を通して，数学の論理や体系に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に積極的に活用しようとする。 数学的活動を通して，数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，よりよく問題を解決する。 数学における基本的な概念，原理・法則，用語・記号などを理解し，知識を身に付けている。

第 ２　各科目の評価の観点の趣旨
　 関心・意欲・態度 数学的な見方や
考え方		 表現・処理 知識・理解
数学基礎 数学的活動を通して，数学と人間のかかわりや社会生活において数学が果たしている役割に関心をもつとともに，数学的な見方や考え方のよさを認識し，数学を事象の考察に活用しようとする。 数学的活動を通して，人間の活動の中で活用されている数学的な見方や考え方に気付き，事象を数理的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 人間の活動の中で活用されている数学を通して，事象を数理的に考察したり，推論の過程を数学的に表現し処理したりする方法を身に付けている。 数学と人間のかかわりや，社会生活において数学が果たしている役割を理解している。
数学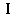1 数学的活動を通して，方程式と不等式，二次関数及び図形と計量における考え方に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に活用しようとする。 数学的活動を通して，方程式と不等式，二次関数及び図形と計量における数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 方程式と不等式，二次関数及び図形と計量において，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，的確に問題を解決する。 方程式と不等式，二次関数及び図形と計量における基本的な概念，原理・法則，用語・記号などを理解し，基礎的な知識を身に付けている。
数学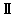2 数学的活動を通して，式と証明・高次方程式，いろいろな関数及び微分・積分の考えにおける考え方や体系に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に進んで活用しようとする。 数学的活動を通して，式と証明・高次方程式，いろいろな関数及び微分・積分の考えにおける数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 式と証明・高次方程式，いろいろな関数及び微分・積分の考えにおいて，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，よりよく問題を解決する。 式と証明・高次方程式，いろいろな関数及び微分・積分の考えにおける基本的な概念，原理・法則，用語・記号などを理解し，基礎的な知識を身に付けている。
数学3 数学的活動を通して，極限，微分法及び積分法における考え方や体系に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に積極的に活用しようとする。 数学的活動を通して，極限，微分法及び積分法における数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り統合的・発展的に考える。 極限，微分法及び積分法において，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，よりよく問題を解決する。 極限，微分法及び積分法における基本的な概念，原理・法則，用語・記号などの理解を深め，知識を身に付けている。
数学Ａ 数学的活動を通して，平面図形，集合と論理及び場合の数と確率における考え方や体系に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に活用しようとする。 数学的活動を通して，平面図形，集合と論理及び場合の数と確率における数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 平面図形，集合と論理及び場合の数と確率において，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，よりよく問題を解決する。 平面図形，集合と論理及び場合の数と確率における基本的な概念，原理・法則，用語・記号などを理解し，基礎的な知識を身に付けている。
数学Ｂ 数学的活動を通して，数列，ベクトル，統計又は数値計算における考え方に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に進んで活用しようとする。 数学的活動を通して，数列，ベクトル，統計又は数値計算における数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 数列，ベクトル，統計又は数値計算において，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，よりよく問題を解決する。 数列，ベクトル，統計又は数値計算における基本的な概念，原理・法則，用語・記号などを理解し，基礎的な知識を身に付けている。
数学Ｃ 数学的活動を通して，行列とその応用，式と曲線，確率分布又は統計処理における考え方に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に積極的に活用しようとする。 数学的活動を通して，行列とその応用，式と曲線，確率分布又は統計処理における数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 行列とその応用，式と曲線，確率分布又は統計処理において，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，よりよく問題を解決する。 行列とその応用，式と曲線，確率分布又は統計処理における基本的な概念，原理・法則，用語・記号などを理解し，知識を身に付けている。


第 ３　必履修科目における内容のまとまりごとの評価規準及びその具体例

1 　数学基礎

１ 　目標
　数学と人間とのかかわりや，社会生活において数学が果たしている役割について理解させ，数学に対する興味・関心を高めるとともに，数学的な見方や考え方のよさを認識し数学を活用する態度を育てる。
２ 　評価の観点の趣旨
関心・意欲・態度 数学的な見方や考え方 表現・処理 知識・理解
数学的活動を通して，数学と人間のかかわりや，社会生活において数学が果たしている役割に関心をもつとともに，数学的な見方や考え方のよさを認識し，数学を事象の考察に活用しようとする。 数学的活動を通して，人間の活動の中で活用されている数学的な見方や考え方に気付き，事象を数理的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考える。 人間の活動の中で活用されている数学を通して，事象を数理的に考察したり，推論の過程を数学的に表現し処理したりする方法を身に付けている。 数学と人間のかかわりや，社会生活において数学が果たしている役割を理解している。

2 　数学1

１ 　目標
　方程式と不等式，二次関数及び図形と計量について理解させ，基礎的な知識の習得と技能の習熟を図り，それらを的確に活用する能力を伸ばすとともに，数学的な見方や考え方のよさを認識できるようにする。
２ 　評価の観点のその趣旨
関心・意欲・態度 数学的な見方や考え方 表現・処理 知識・理解
数学的活動を通して，方程式と不等式，二次関数及び図形と計量における考え方に関心をもつとともに，数学的な見方や考え方のよさを認識し，それらを事象の考察に活用しようとする。 数学的活動を通して，方程式と不等式，二次関数及び図形と計量における数学的な見方や考え方を身に付け，事象を数学的にとらえ，論理的に考えるとともに思考の過程を振り返り多面的・発展的に考 方程式と不等式，二次関数及び図形と計量において，事象を数学的に考察し，表現し処理する仕方や推論の方法を身に付け，的確に問題を解決する。 方程式と不等式，二次関数及び図形と計量における基本的な概念，原理・法則，用語・記号などを理解し，基礎的な知識を身に付けている。


３ 　学習指導要領の内容，内容のまとまりごとの評価規準及びその具体例

　数学1においては，学習指導要領の内容の（１）や（２）などの大項目を内容のまとまりとして，それぞれについて評価規準を作成した。

(2) 　「（２）二次関数」
【 学習指導要領の内容】
　二次関数について理解し，関数を用いて数量の変化を表現することの有用性を認識するとともに，それを具体的な事象の考察や二次不等式を解くことなどに活用できるようにする。
ア 　二次関数とそのグラフ
イ 　二次関数の値の変化
（ア） 二次関数の最大・最小
（イ） 二次不等式

【 「（２）二次関数」の評価規準】
関心・意欲・態度 数学的な見方や考え方 表現・処理 知識・理解
二次関数とそのグラフや値の変化に関心をもつとともに，関数を用いて数量の変化を表現することの有用性を認識し，二次関数を活用しようとする。 関数的な見方や考え方を身に付け，具体的な事象について関数を用いて考察することができる。 関数を用いて数量の変化を表現し，関数の値の変化を調べることができる。 二次関数とそのグラフ及び関数の値の変化における基本的な概念，原理・法則，用語・記号などを理解し，基礎的な知識を身に付けている。

【 「（２）二次関数」の評価規準の具体例】
関心・意欲・態度 数学的な見方や考え方 表現・処理 知識・理解
【 二次関数とそのグラフ】
・ 具体的な事象の中にある二つの数量の関係に関心をもつ。
・ 二次関数とそのグラフについて関心をもち，調べようとする。

・ 二つの数量の関係を表，式，グラフなどを用いて考察することができる。



・ いろいろな事象を表す関数について，いくつかの点をとってグラフに表すことができる。
・ 二次関数ワイ イコール エイ エックス ２乗プラス ビー エックス プラス シーのグラフとワイ イコール エイ エックス ２乗のグラフの位置関係を調べることができる。

・ いろいろな事象を表す関数や二次関数について理解し，基礎的な知識を身に付けている。
【 二次関数の値の変化】
・ 二次関数の値の変化に関心をもち，具体的な事象の考察に二次関数の最大・最小を活用しようとする。
・ 二次不等式の解に関心をもち，二次関数のグラフを活用して二次不等式の解を求めようとする。

・ 二次関数の値の変化の様子について，グラフを用いて考察することができる。
・ 二次不等式の解を二次関数のグラフを用いて考察することができる。

・ 二次関数のグラフや式を用いて，二次関数の最大値・最小値を求めることができる。
・ 二次関数のグラフを活用して二次不等式の解を求めることができる。

・ 二次関数の最大値・最小値とその求め方について理解し，基礎的な知識を身に付けている。
・ 二次不等式の解の意味を二次関数のグラフとの関係から理解している。



ページの先頭へ   文部科学省ホームページのトップへ